题目内容
(本小题满分14分)
已知椭圆的两 个焦点
个焦点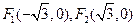 ,过
,过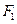 且与坐标轴不平行的直线
且与坐标轴不平行的直线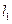 与椭圆相交于M,N两点,如果
与椭圆相交于M,N两点,如果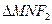 的周长等于8.
的周长等于8.
(I)求椭圆的方程;
(Ⅱ)若过点(1,0)的直线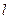 与椭圆交于不同两点P、Q,试问在
与椭圆交于不同两点P、Q,试问在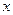 轴上是否存在定点E(
轴上是否存在定点E(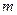 ,0),使
,0),使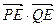 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
已知椭圆的两
 个焦点
个焦点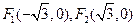 ,过
,过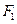 且与坐标轴不平行的直线
且与坐标轴不平行的直线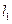 与椭圆相交于M,N两点,如果
与椭圆相交于M,N两点,如果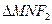 的周长等于8.
的周长等于8.(I)求椭圆的方程;
(Ⅱ)若过点(1,0)的直线
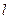 与椭圆交于不同两点P、Q,试问在
与椭圆交于不同两点P、Q,试问在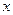 轴上是否存在定点E(
轴上是否存在定点E(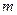 ,0),使
,0),使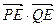 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.(1)
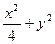 ="1"
="1" (2)
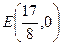 时,
时,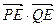 为定值
为定值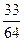
解:(I)由题意知 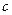 =
=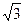 ,
,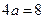 ,(2分)∴
,(2分)∴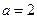 ,
,  =1
=1
∴椭圆的方程为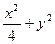 ="1" (4分)
="1" (4分)
(II)当直线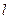 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为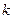 ,则
,则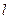 的方程为
的方程为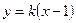
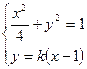 消去
消去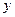 得
得 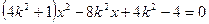 (6分)
(6分)
设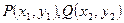
则由韦达定理得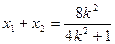
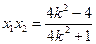
 (7分)
(7分)
则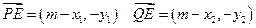
∴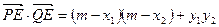 =
=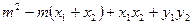
=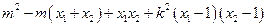
=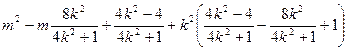
=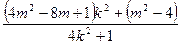 (10分)
(10分)
要使上式为定值须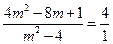 ,解得
,解得 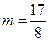
∴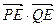 为定值
为定值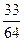 (12分)当直线
(12分)当直线 的斜率不存在时
的斜率不存在时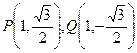 由
由
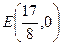
可得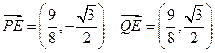
∴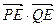 =
=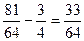 综上所述当
综上所述当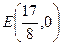 时,
时,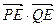 为定值
为定值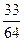 (14分)
(14分)
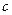 =
=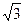 ,
,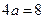 ,(2分)∴
,(2分)∴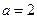 ,
,  =1
=1∴椭圆的方程为
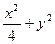 ="1" (4分)
="1" (4分)(II)当直线
 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为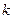 ,则
,则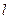 的方程为
的方程为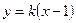
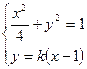 消去
消去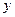 得
得 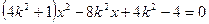 (6分)
(6分)设
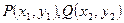
则由韦达定理得
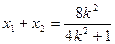
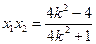
 (7分)
(7分)则
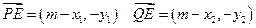
∴
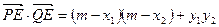 =
=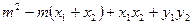
=
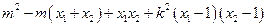
=
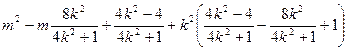
=
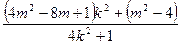 (10分)
(10分)要使上式为定值须
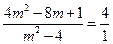 ,解得
,解得 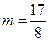
∴
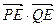 为定值
为定值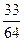 (12分)当直线
(12分)当直线 的斜率不存在时
的斜率不存在时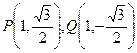 由
由
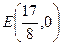
可得
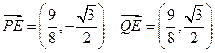
∴
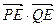 =
=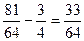 综上所述当
综上所述当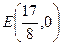 时,
时,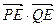 为定值
为定值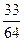 (14分)
(14分)
练习册系列答案
相关题目
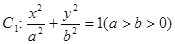 的左准线为
的左准线为 ,左右焦点分别为
,左右焦点分别为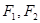 ,抛物线
,抛物线 的准线为
的准线为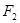 ,曲线
,曲线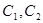 的一个交点为P,则
的一个交点为P,则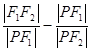 等于()
等于()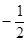 D
D 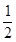
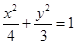 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则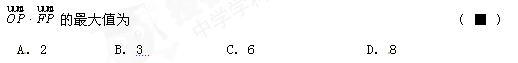
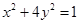 的离心率为( )
的离心率为( )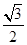
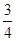
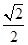
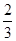
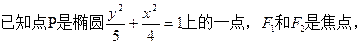
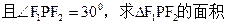 .
.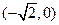 ,
,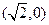 ,离心率是
,离心率是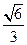 ,直线
,直线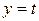 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。 的值;
的值;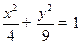 的上、下两个焦点分别为
的上、下两个焦点分别为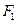 、
、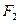 ,点
,点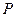 为该椭圆上一点,若
为该椭圆上一点,若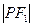 、
、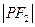 为方程
为方程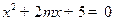 的两根,则
的两根,则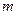 =" " .
=" " .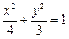 ,则直线
,则直线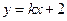 与椭圆至多有一个公共点的充要条件
与椭圆至多有一个公共点的充要条件