题目内容
若对任意x∈R,不等式x2≥2ax-1恒成立,则实数a的取值范围是
[-1,1]
[-1,1]
.分析:由已知,不等式x2-2ax+1≥0恒成立,根据二次函数图象与二次不等式解的关系可知须△≤0,解此不等式即可.
解答:解:不等式x2≥2ax-1恒成立,即不等式x2-2ax+1≥0恒成立.∵x2的系数1>0,∴△=4a2-4≤0,即a2≤1,解得a∈[-1,1].
故答案为:[-1,1].
故答案为:[-1,1].
点评:本题考查不等式(函数)恒成立问题.由于本题是二次不等式,故采用数形结合的思想,利用根据二次函数图象与二次不等式解的关系来解决.要掌握好“三个二次”的关系,以及其中蕴含的数形结合、转化的思想方法.

练习册系列答案
相关题目
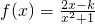 的定义域为[α,β].
的定义域为[α,β].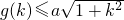 成立,
成立,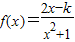 的定义域为[α,β].
的定义域为[α,β].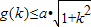 成立,
成立,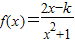 的定义域为[α,β].
的定义域为[α,β].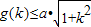 成立,
成立,