题目内容
(本小题满分16分)
已知数列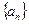 满足,
满足,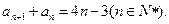
(1)若数列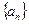 是等差数列,求
是等差数列,求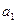 的值;
的值;
(2)当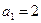 时,求数列
时,求数列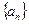 的前n项和
的前n项和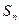 ;
;
(3)若对任意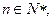 都有
都有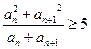 成立,求
成立,求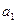 的取值范围.
的取值范围.
已知数列
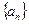 满足,
满足,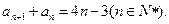
(1)若数列
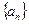 是等差数列,求
是等差数列,求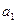 的值;
的值;(2)当
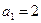 时,求数列
时,求数列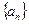 的前n项和
的前n项和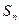 ;
;(3)若对任意
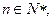 都有
都有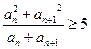 成立,求
成立,求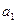 的取值范围.
的取值范围.(1)
(2)略
(3) 的取值范围是
的取值范围是

(2)略
(3)
 的取值范围是
的取值范围是
解:(1)若数列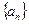 是等差数列,则
是等差数列,则
由 得
得 即
即
解得, ……………………4分
……………………4分
(2)由 得
得

两式相减,得
所以数列 是首项为
是首项为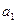 ,公差为4的等差数.
,公差为4的等差数.
数列 是首项为
是首项为 ,公差为4的等差数列,
,公差为4的等差数列,
由
所以 ……………………6分
……………………6分
①当





 ……………………8分
……………………8分
②当 为偶数时,
为偶数时,


 ……………………10分
……………………10分
(3)由(2)知,
①当 为奇数时,
为奇数时,
由
令
当
解得 ……………………13分
……………………13分
②当 为偶数时,
为偶数时,
由
令
当 时,
时,
解得
综上, 的取值范围是
的取值范围是 ………………16分
………………16分
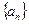 是等差数列,则
是等差数列,则
由
 得
得 即
即
解得,
 ……………………4分
……………………4分(2)由
 得
得

两式相减,得

所以数列
 是首项为
是首项为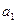 ,公差为4的等差数.
,公差为4的等差数.数列
 是首项为
是首项为 ,公差为4的等差数列,
,公差为4的等差数列,由

所以
 ……………………6分
……………………6分①当






 ……………………8分
……………………8分②当
 为偶数时,
为偶数时,

 ……………………10分
……………………10分(3)由(2)知,

①当
 为奇数时,
为奇数时,
由

令

当

解得
 ……………………13分
……………………13分②当
 为偶数时,
为偶数时,
由

令

当
 时,
时,
解得

综上,
 的取值范围是
的取值范围是 ………………16分
………………16分
练习册系列答案
相关题目
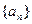 满足:
满足: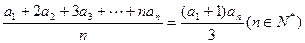
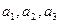 的值,猜测
的值,猜测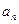 的表达式并给予证明;
的表达式并给予证明;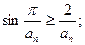
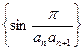 的前n项和为
的前n项和为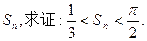
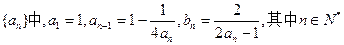 。
。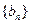 是等差数列,并求数列
是等差数列,并求数列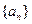 的通项公式
的通项公式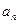 ;
;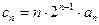 ,求数列
,求数列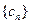 的前
的前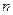 项和。
项和。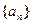 满足:
满足: 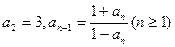 , 则
, 则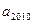 =" " ( )
=" " ( )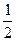
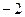
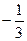
 成等比数列,则该等比数列的公比为 。
成等比数列,则该等比数列的公比为 。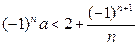 对于任意正整数n恒成立,则实数a的取值范围是
对于任意正整数n恒成立,则实数a的取值范围是 中,若
中,若 ,则
,则
 ,0)
,0) (0,1)
(0,1) 单位长度,那么第2010秒时,这个粒子所在的位置为( )
单位长度,那么第2010秒时,这个粒子所在的位置为( ) 

 是公差不为
是公差不为 的等差数列,
的等差数列, 且
且 、
、 、
、 成等比数列,则
成等比数列,则 项和
项和 等于( )
等于( ) .
.
 .
.
 .
.

