题目内容
 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
- A.1
- B.2
- C.2

- D.4
B
分析:由题意画出过正方体的两条相对侧棱的截面图,设出正方体的棱长,然后利用A点的纵坐标相等列式求解a的值.
解答: 解:作过正方体的两条相对侧棱的截面图如图,
解:作过正方体的两条相对侧棱的截面图如图,
设正方体AC1的棱长AA1=a,则底面对角线AC= ,
,
所以A点的横坐标等于 ,代入抛物线y=x2得:
,代入抛物线y=x2得: ,
,
即A点纵坐标为 .
.
又由题意可知A点纵坐标等于4-a.
所以 ,解得:a=2.
,解得:a=2.
所以正方体的棱长是2.
故选B.
点评:本题考查了抛物线的应用,考查了数形结合的解题思想和数学转化思想,能够正确作出该题的截面图是解答该题的关键,属中档题.
分析:由题意画出过正方体的两条相对侧棱的截面图,设出正方体的棱长,然后利用A点的纵坐标相等列式求解a的值.
解答:
 解:作过正方体的两条相对侧棱的截面图如图,
解:作过正方体的两条相对侧棱的截面图如图,设正方体AC1的棱长AA1=a,则底面对角线AC=
 ,
,所以A点的横坐标等于
 ,代入抛物线y=x2得:
,代入抛物线y=x2得: ,
,即A点纵坐标为
 .
.又由题意可知A点纵坐标等于4-a.
所以
 ,解得:a=2.
,解得:a=2.所以正方体的棱长是2.
故选B.
点评:本题考查了抛物线的应用,考查了数形结合的解题思想和数学转化思想,能够正确作出该题的截面图是解答该题的关键,属中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知不等式组
表示平面区域D,现在往抛物线y=-x2+x+2与x轴围成的封闭区域内随机地抛掷一小颗粒,则该颗粒落到区域D中的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的表面积是( )
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的表面积是( )A、96-48
| ||
| B、32 | ||
| C、24 | ||
D、144-48
|
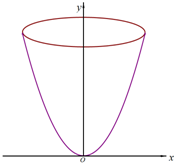 (2013•大兴区一模)抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
(2013•大兴区一模)抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( ) 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是