题目内容
△ABC的顶点A(2,4),B(-1,2),C(1,0),点P(x,y)在△ABC内部及其边界上运动,则z=x-y的最大值与最小值分别为
- A.3,1
- B.-1,-3
- C.1,-3
- D.3,-1
C
分析:①画三角形ABC②目标函数z为直线纵截距相反数纵截距最大z最小.纵截距最小z最大.③平移直线z=x-y,区分一下直线AB的斜率与1的大小关系,确定在点C还是点B取最值.
解答: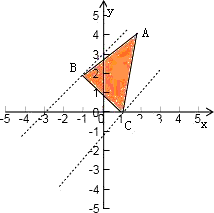 解;由A、B、C三点的坐标找出可行域,
解;由A、B、C三点的坐标找出可行域,
先作直线x-y=0,对该直线进行平移,
可以发现经过点B时z取得最小值-3,
经过点C时z取得最大值1
则z=x-y的最大值为 1最小值为-3;
故选C.
点评:本题主要考查了简单的线性规划,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.
分析:①画三角形ABC②目标函数z为直线纵截距相反数纵截距最大z最小.纵截距最小z最大.③平移直线z=x-y,区分一下直线AB的斜率与1的大小关系,确定在点C还是点B取最值.
解答:
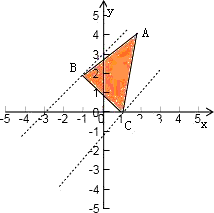 解;由A、B、C三点的坐标找出可行域,
解;由A、B、C三点的坐标找出可行域,先作直线x-y=0,对该直线进行平移,
可以发现经过点B时z取得最小值-3,
经过点C时z取得最大值1
则z=x-y的最大值为 1最小值为-3;
故选C.
点评:本题主要考查了简单的线性规划,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
相关题目
数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标是( )
| A、(-4,0) | B、(0,-4) | C、(4,0) | D、(4,0)或(-4,0) |