题目内容
已知曲线C上的动点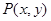 满足到定点
满足到定点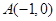 的距离与到定点
的距离与到定点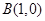 距离之比为
距离之比为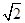 .
.
(1)求曲线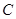 的方程;
的方程;
(2)过点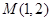 的直线
的直线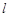 与曲线
与曲线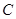 交于两点
交于两点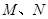 ,若
,若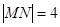 ,求直线
,求直线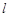 的方程.
的方程.
(1) 或
或 ;(2)
;(2) 或
或 .
.
解析试题分析:(1)根据动点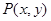 满足到定点
满足到定点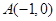 的距离与到定点
的距离与到定点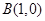 距离之比为
距离之比为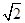 ,建立方程,化简可得曲线
,建立方程,化简可得曲线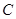 的方程;(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线
的方程;(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线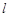 的方程.
的方程.
(1)由题意得 =
=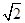
 ,
,
故 ,
,
化简得: (或
(或 )即为所求.
)即为所求.
(2)当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 ,
,
将 代入方程
代入方程 得
得 ,
,
所以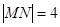 ,满足题意.
,满足题意.
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 +2,
+2,
由圆心到直线的距离 ,
,
解得 ,此时直线
,此时直线 的方程为
的方程为 .
.
综上所述,满足题意的直线 的方程为:
的方程为: 或
或 .
.
考点:1、两点的距离公式;2、点到直线的距离;3、直线与圆的方程.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
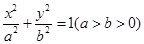 上的点到椭圆右焦点
上的点到椭圆右焦点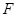 的最大距离为
的最大距离为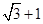 ,离心率
,离心率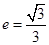 ,直线
,直线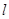 过点
过点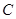 交于
交于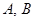 两点.
两点.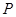 ,使得当
,使得当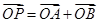 成立?若存在,求出所有点
成立?若存在,求出所有点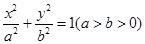 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率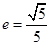 , 直线
, 直线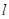 交椭圆于M,N两点.
交椭圆于M,N两点. BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线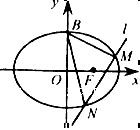
 :
: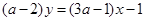
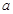 取何值,直线
取何值,直线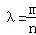 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.