题目内容
已知数列 满足
满足 ,数列
,数列 满足
满足 .
.
(Ⅰ)证明数列 是等差数列并求数列
是等差数列并求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ) 用等差数列的定义来证明,然后根据通项公式来求;(Ⅱ)利用错位相减来求和.
试题解析:(I)证明:由 ,得
,得 ,
,
∴
所以数列 是等差数列,首项
是等差数列,首项 ,公差为
,公差为
∴
(II)

 ----①
----①
 -------------------②
-------------------②
①-②得



考点:等差数列的证明以及通项公式和前 项和公式、错位相减的求和
项和公式、错位相减的求和

练习册系列答案
相关题目
 中,
中,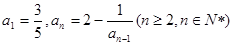 ,数列
,数列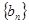 满足
满足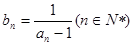 。
。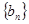 前
前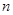 项和
项和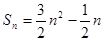 .数列
.数列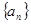 满足
满足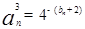
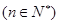 ,数列
,数列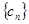 满足
满足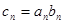 。
。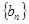 的通项公式;
的通项公式;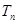 ;
;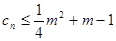 对一切正整数
对一切正整数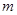 的取值范围。
的取值范围。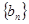 前
前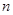 项和
项和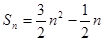 .数列
.数列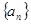 满足
满足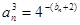
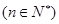 ,数列
,数列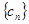 满足
满足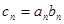 。(1)求数列
。(1)求数列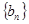 的通项公式;(2)求数列
的通项公式;(2)求数列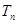 ;(3)若
;(3)若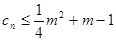 对一切正整数
对一切正整数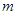 的取值范围。
的取值范围。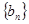 前
前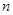 项和
项和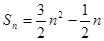 .数列
.数列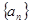 满足
满足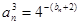
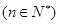 ,数列
,数列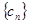 满足
满足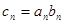 。
。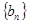 的通项公式;
的通项公式;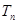 ;
;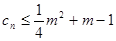 对一切正整数
对一切正整数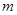 的取值范围。
的取值范围。