题目内容
设x，y为正数，且x，a1，a2，y成等差数列，x，b1，b2，y成等比数列，则
的最小值是 ．
【答案】分析：先利用条件得到a1+a2=x+y和b1b2=xy，再对所求都转化为用x，y表示后，在用基本不等式可得结论．
解答：解：由等差数列的性质知a1+a2=x+y；
由等比数列的性质知b1b2=xy，
所以
，
当且仅当x=y时取等号．
故答案为：4．
点评：本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力，考查归化与转化思想．
解答：解：由等差数列的性质知a1+a2=x+y；
由等比数列的性质知b1b2=xy，
所以
，当且仅当x=y时取等号．
故答案为：4．
点评：本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力，考查归化与转化思想．
练习册系列答案
阅读快车系列答案
相关题目
≤a恒成立的a的最小值是
B.
C.2 D.2
，求函数f（x）的最小值；
+
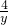的最小值．
的最小值是 ．