题目内容
(1)已知函数 ,求函数f(x)的最小值;
,求函数f(x)的最小值;
(2)设x,y为正数,且x+y=1,求 +
+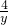 的最小值.
的最小值.
解:(1)∵x∈(0,+∞),∴f(x)=x+ +2
+2 =4,当且仅当
=4,当且仅当 ,x>0,即x=1时取等号,故函数f(x)的最小值为4;
,x>0,即x=1时取等号,故函数f(x)的最小值为4;
(2)∵x>0,y>0,x+y=1,
∴ =
= =5+
=5+ ≥
≥ =9,当且仅当
=9,当且仅当 ,x+y=1,x>0,y>0,即
,x+y=1,x>0,y>0,即 ,y=
,y= 时取等号,即
时取等号,即 的最小值为9.
的最小值为9.
分析:(1)利用基本不等式求出即可;
(2)利用“乘1法”,使用基本不等式即可.
点评:变形使用基本不等式是解题的关键.
 +2
+2 =4,当且仅当
=4,当且仅当 ,x>0,即x=1时取等号,故函数f(x)的最小值为4;
,x>0,即x=1时取等号,故函数f(x)的最小值为4;(2)∵x>0,y>0,x+y=1,
∴
 =
= =5+
=5+ ≥
≥ =9,当且仅当
=9,当且仅当 ,x+y=1,x>0,y>0,即
,x+y=1,x>0,y>0,即 ,y=
,y= 时取等号,即
时取等号,即 的最小值为9.
的最小值为9.分析:(1)利用基本不等式求出即可;
(2)利用“乘1法”,使用基本不等式即可.
点评:变形使用基本不等式是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值. ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为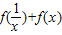 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.