题目内容
求证:如果一个平面经过一条线段的中点,那么这条线段的两个端点到平面的距离相等.
见解析
已知:线段AB的中点为O,O∈平面α.
求证:A、B两点到平面α的距离相等.
证明:(1)当线段在平面α上时,A、B两点显然到平面α的距离相等且为0.
(2)当线段AB不在平面α上时,作AA1⊥α,BB1⊥α,A1和B1为垂足,则AA1,BB1分别是A、B到平面α的距离;且AA1∥BB1,AA1、BB1确定平面β,β∩α=A1B1
∵O∈AB,,AB
 β
β∴O∈β,又O∈α
∴O∈A1B1
∴AA1⊥A1O,BB1⊥B1O
∵∠AOA1=∠BOB1,AO=BO
∴Rt△AA1O≌Rt△BB1O
∴AA1=BB1,即线段AB的两个端点到平面α的距离相等.

练习册系列答案
相关题目
 中,
中, ,二面角
,二面角 的大小等于
的大小等于 ,
, 到面
到面 的距离等于
的距离等于 ,
, 到面
到面 的距离等于
的距离等于 ,则直线
,则直线 与直线
与直线


 中,
中,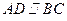 且
且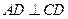 ;平面
;平面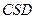
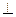 平面
平面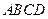 ,
,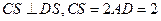 ;
;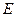 为
为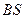 的中点,
的中点,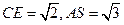 。求:
。求: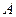 到平面
到平面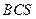 的距离;
的距离;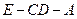 的大小。
的大小。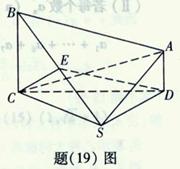
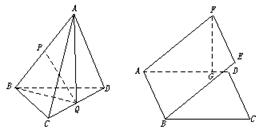
 中,
中, ,
, ,
, 点在直线
点在直线 上,若
上,若 ,求出点
,求出点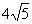
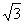
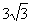
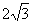
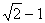
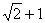
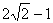
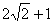
 到直线
到直线 的距离等于( )
的距离等于( )



 中,
中, ,它所在平面外一点
,它所在平面外一点 到
到 的距离是 .
的距离是 .