题目内容
已知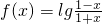 .
.
(Ⅰ)求证: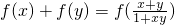 ;
;
(Ⅱ)若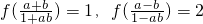 ,求f(a)和f(b)的值.
,求f(a)和f(b)的值.
解:(1)证明:∵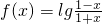 ,
,
∴ =
= ,
,
∴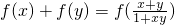 成立.
成立.
(2)由已知可证f(-x)=-f(x),再由(1)得 ,
,
解得 ,
, .
.
分析:(1)利用对数的运算性质化简要证等式的左边,结果等于等式的右边,从而证得等式成立.
(2)由已知可证f(-x)=-f(x),再由(1)得 ,解方程组求得f(a)和f(b)的值.
,解方程组求得f(a)和f(b)的值.
点评:本题主要考查对数的运算性质的应用,求函数的值,式子的变形,是解题的关键,属于基础题.
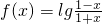 ,
,∴
 =
= ,
,∴
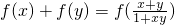 成立.
成立.(2)由已知可证f(-x)=-f(x),再由(1)得
 ,
,解得
 ,
, .
.分析:(1)利用对数的运算性质化简要证等式的左边,结果等于等式的右边,从而证得等式成立.
(2)由已知可证f(-x)=-f(x),再由(1)得
 ,解方程组求得f(a)和f(b)的值.
,解方程组求得f(a)和f(b)的值.点评:本题主要考查对数的运算性质的应用,求函数的值,式子的变形,是解题的关键,属于基础题.

练习册系列答案
相关题目
 如图,已知长方体ABCD-A1B1C1D1.求证:平面AB1D1∥平面BDC1.
如图,已知长方体ABCD-A1B1C1D1.求证:平面AB1D1∥平面BDC1.