题目内容
在 中,角A,B,C所对应的边分别为
中,角A,B,C所对应的边分别为 ,则
,则 是
是 的( )
的( )
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
A
解析试题分析:判断条件的充要性,需正反两面性证明(即充分性和必要性证明)由。充分性:正弦定理 ,
,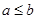 可得
可得 ,充分条件得证。必要性:因在
,充分条件得证。必要性:因在 内
内 ,
, ,则
,则 ,由“大角对大边”可得
,由“大角对大边”可得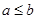 。故
。故 是
是 充要条件。
充要条件。
考点:正弦定理,三角形内角和定理,充要条件概念

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知命题p: x∈R,x2+x-6
x∈R,x2+x-6 0,则命题
0,则命题 P是( )
P是( )
A. x∈R,x2+x-6>0 x∈R,x2+x-6>0 | B. x∈R.x2+x-6>0 x∈R.x2+x-6>0 |
C. x∈R,x2+x-6>0 x∈R,x2+x-6>0 | D. x∈R.x2+x-6<0 x∈R.x2+x-6<0 |
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当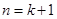 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
A.当 时,该命题不成立 时,该命题不成立 | B.当 时,该命题成立 时,该命题成立 |
C.当 时,该命题成立 时,该命题成立 | D.当 时,该命题不成立 时,该命题不成立 |
在 中,角
中,角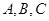 所对应的边分别为
所对应的边分别为 ,则
,则 是
是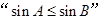 的( ).
的( ).
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
命题“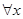 ∈R,
∈R,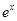 -x+1≥0”的否定是( )
-x+1≥0”的否定是( )
A.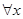 ∈R,lnx+x+1<0 ∈R,lnx+x+1<0 | B.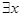 ∈R, ∈R,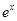 -x+1<0 -x+1<0 |
C.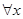 ∈R, ∈R,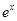 -x+1>0 -x+1>0 | D.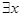 ∈R, ∈R,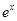 -x+1≥0 -x+1≥0 |
设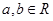 ,则“
,则“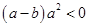 ”是“
”是“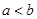 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
集合 ,则
,则 =( )
=( )
| A.{1,2} | B.{0,1,2} | C.{1,2,3} | D.{0,1,2,3} |
 只有一个元素,
只有一个元素, ,
, .
. 的取值范围
的取值范围
 的关系.
的关系. 的定义域为集合N,求:
的定义域为集合N,求: