题目内容
设f(x)=|logax|,其中a>1,则f(2),f(
),f(
)由大到小排列为 .
| 1 |
| 3 |
| 1 |
| 4 |
分析:作出函数f(x)=|logax|,其中a>1的图象,再根据f(2)=f(
),结合函数f(x)=|logax|在(0,1)上单调性可判断f(2),f(
),f(
)的大小关系.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
解答: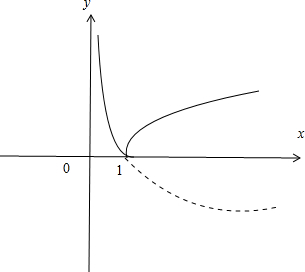 解:∵函数f(x)=|logax|,其中a>1,
解:∵函数f(x)=|logax|,其中a>1,
∴f(2)=|loga2|=|-loga2|=|loga
|=f(
).
化出函数f(x)的单调性示意图,如图所示:
再根据函数f(x)在(0,1)上单调递减,且
>
>
,
可得f(
)>f(
)>f(2),
故答案为:f(
)>f(
)>f(2).
 解:∵函数f(x)=|logax|,其中a>1,
解:∵函数f(x)=|logax|,其中a>1,∴f(2)=|loga2|=|-loga2|=|loga
| 1 |
| 2 |
| 1 |
| 2 |
化出函数f(x)的单调性示意图,如图所示:
再根据函数f(x)在(0,1)上单调递减,且
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
可得f(
| 1 |
| 4 |
| 1 |
| 3 |
故答案为:f(
| 1 |
| 4 |
| 1 |
| 3 |
点评:本题主要考查了利用对数函数的单调性比较对数值的大小,解答本题的关键是要根据对数函数的图象及函数的图象变换准确作出函数f(x)的图象,体现了数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
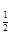 (
(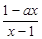 )为奇函数,a为常数.
)为奇函数,a为常数.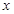 的值,不等式
的值,不等式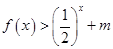 恒成立,求实数
恒成立,求实数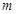 的取值范围.
的取值范围.
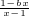 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.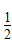
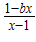 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.