题目内容
设f(x)=log
为奇函数,b为常数.
(1)求b的值;
(2)求f(2)+f(3)+…+f(9)+f(10)的值;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>(
)x+m恒成立,求实数m的取值范围.
| 1 |
| 2 |
| 1-bx |
| x-1 |
(1)求b的值;
(2)求f(2)+f(3)+…+f(9)+f(10)的值;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>(
| 1 |
| 2 |
分析:(1)由f(x)=log
为奇函数,知log
+log
=log
=0,由此能求出b.
(2)由f(x)=log
,知f(2)+f(3)+…+f(9)+f(10)=log
,由此能求出结果.
(3)对于区间[3,4]上的每一个x的值,不等式f(x)>(
)x+m恒成立,等价于当x∈[3,4]时,f(x)-(
)x=log
-(
)x恒成立,设h(x)=log
-(
)x=log2
-(
)x,推导出y=h(x)在[3,4]上单调递增,由此能求出实数m的取值范围.
| 1 |
| 2 |
| 1-bx |
| x-1 |
| 1 |
| 2 |
| 1+bx |
| -x-1 |
| 1 |
| 2 |
| 1-bx |
| x-1 |
| 1 |
| 2 |
| 1-b2x2 |
| 1-x2 |
(2)由f(x)=log
| 1 |
| 2 |
| x+1 |
| x-1 |
| 1 |
| 2 |
| 3×4×…×9×10×11 |
| 1×2×3×…×9 |
(3)对于区间[3,4]上的每一个x的值,不等式f(x)>(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x-1 |
| x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| x-1 |
| x+1 |
| 1 |
| 2 |
| x+1 |
| x-1 |
| 1 |
| 2 |
解答:解:(1)∵f(x)=log
为奇函数,b为常数,
∴f(-x)+f(x)=0,
∴log
+log
=log
=0,
∴
=1,解得b=±1.
∵b=1时,
=-1,不成立,舍去,∴b=-1.
(2)∵b=-1,∴f(x)=log
,
∴f(2)+f(3)+…+f(9)+f(10)
=log
+log
+…+log
+log
=log
=log
=log
55.
(3)∵对于区间[3,4]上的每一个x的值,不等式f(x)>(
)x+m恒成立,
∴当x∈[3,4]时,f(x)-(
)x=log
-(
)x恒成立,
设h(x)=log
-(
)x=log2
-(
)x,
∵y=log2
=log2(1-
)在[3,4]上单调递增,y=(
)x在[3,4]上单调递减,
∴y=h(x)在[3,4]上单调递增,
∴只需m<h(3)=log
-(
)3=-
,
∴m<-
.
故实数m的取值范围是(-∞,-
).
| 1 |
| 2 |
| 1-bx |
| x-1 |
∴f(-x)+f(x)=0,
∴log
| 1 |
| 2 |
| 1+bx |
| -x-1 |
| 1 |
| 2 |
| 1-bx |
| x-1 |
| 1 |
| 2 |
| 1-b2x2 |
| 1-x2 |
∴
| 1-b2x2 |
| 1-x2 |
∵b=1时,
| 1-bx |
| x-1 |
(2)∵b=-1,∴f(x)=log
| 1 |
| 2 |
| x+1 |
| x-1 |
∴f(2)+f(3)+…+f(9)+f(10)
=log
| 1 |
| 2 |
| 3 |
| 1 |
| 1 |
| 2 |
| 4 |
| 2 |
| 1 |
| 2 |
| 10 |
| 8 |
| 1 |
| 2 |
| 11 |
| 9 |
=log
| 1 |
| 2 |
| 3×4×…×9×10×11 |
| 1×2×3×…×9 |
=log
| 1 |
| 2 |
| 10×11 |
| 1×2 |
=log
| 1 |
| 2 |
(3)∵对于区间[3,4]上的每一个x的值,不等式f(x)>(
| 1 |
| 2 |
∴当x∈[3,4]时,f(x)-(
| 1 |
| 2 |
| 1 |
| 2 |
| x-1 |
| x+1 |
| 1 |
| 2 |
设h(x)=log
| 1 |
| 2 |
| x-1 |
| x+1 |
| 1 |
| 2 |
| x+1 |
| x-1 |
| 1 |
| 2 |
∵y=log2
| x-1 |
| x+1 |
| 2 |
| x+1 |
| 1 |
| 2 |
∴y=h(x)在[3,4]上单调递增,
∴只需m<h(3)=log
| 1 |
| 2 |
| 3+1 |
| 3-1 |
| 1 |
| 2 |
| 9 |
| 8 |
∴m<-
| 9 |
| 8 |
故实数m的取值范围是(-∞,-
| 9 |
| 8 |
点评:本题考查满足条件的实数值的求法,考查对数值的计算,考查满足条件的实数的取值范围的求法,综合性强,难度大.解题时要注意函数的奇偶性、单调性和构造法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
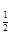 (
(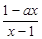 )为奇函数,a为常数.
)为奇函数,a为常数.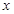 的值,不等式
的值,不等式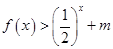 恒成立,求实数
恒成立,求实数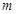 的取值范围.
的取值范围.
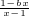 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.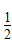
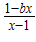 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.