Question

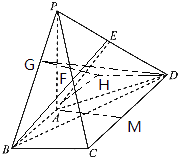
【题目】如图，四棱锥P﹣ABCD的底面是直角梯形，∠ABC=∠BCD= ，AB=BC=1，CD=2，PA⊥平面ABCD，E是PD的中点．

（1）求证：AE∥平面PBC；
（2）若直线AE与直线BC所成角等于 ，求二面角D﹣PB﹣A平面角的余弦值．

Answer 1

【答案】
（1）证明：取PC中点F，连结EF、BF，

∴△PCD中，EF ，AB ，

∴EF AB，

∴四边形ABFE为平行四边形，

∵AE∥BF，AE平面PBC，BF平面PBC，

∴AE∥平面PBC．

（2）解：AE与直线BC所成角为 ， ，

∴BP= ，∴PA= ，

延长BA一倍到H，连结DH，再作HG⊥BP，连结DG，

则∠DGH是二面角D﹣PB﹣A的平面角，

DH=1，FG× ，HG= ，

∴tan∠DGH= ，

∴cos∠DGH= ．

∴二面角D﹣PB﹣A平面角的余弦值为 ．

【解析】（1）取PC中点F，连结EF、BF，推导出四边形ABFE为平行四边形，从而AE∥BF，由此能证明AE∥平面PBC．（2）AE与直线BC所成角为 ，延长BA一倍到H，连结DH，再作HG⊥BP，连结DG，∠DGH是二面角D﹣PB﹣A的平面角，由此能求出二面角D﹣PB﹣A平面角的余弦值．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．