题目内容
已知数列an的前n项和为Sn,a1=1且3an+1+2sn=3(n为正整数)
(1)求数列an的通项公式;
(2)记S=a1+a2+…+an+….若对任意正整数n,kS≤Sn恒成立,求实数k的最大值.
解:(1)由题设条件得
3an+1+2sn=3,3an+2sn-1=3
两式相减,得3an+1-3an+2(Sn-Sn-1)=0,
即 ,n>1 又
,n>1 又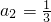 ,
,
所以通项为: .
.
(2)S= =
= ,
,
要kS≤Sn恒成立,由于Sn递增
所以只要kS=S1,即k的最大值为 .
.
分析:(1)3an+1+2sn=3,3an+2sn-1=3,两式相减,得3an+1-3an+2(Sn-Sn-1)=0,由此能求出数列{an}的通项公式.
(2)S= =
= ,由此能求出k的最大值.
,由此能求出k的最大值.
点评:本题考查数列的递推式和数列性质的综合应用,解题时要认真审题,仔细解答,注意不等式和数列的综合应用.
3an+1+2sn=3,3an+2sn-1=3
两式相减,得3an+1-3an+2(Sn-Sn-1)=0,
即
 ,n>1 又
,n>1 又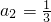 ,
,所以通项为:
 .
.(2)S=
 =
= ,
,要kS≤Sn恒成立,由于Sn递增
所以只要kS=S1,即k的最大值为
 .
.分析:(1)3an+1+2sn=3,3an+2sn-1=3,两式相减,得3an+1-3an+2(Sn-Sn-1)=0,由此能求出数列{an}的通项公式.
(2)S=
 =
= ,由此能求出k的最大值.
,由此能求出k的最大值.点评:本题考查数列的递推式和数列性质的综合应用,解题时要认真审题,仔细解答,注意不等式和数列的综合应用.

练习册系列答案
相关题目