题目内容
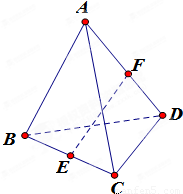
如图,空间四边形ABCD中,四边AB、BC、CD、DA和对角线AC、BD都等于a,E、F分别为AB、CD的中点.
(1)求证:EF是异面直线AB、CD的公垂线;
(2)求异面直线AB和CD的距离.
(1)证明:如图,连结AF、BF,
由已知△BCD和△ACD均为正三角形,
E、F分别为AB、CD的中点,
∴AF=BF,EF⊥AB.
同理,EF⊥CD.
又EF与AB、CD都相交,
∴EF为异面直线AB、CD的公垂线.
(2)解:∵空间四边形各边及对角线AC、BD的长均为a,
∴AF=BF=
.而AE=
,
∴在Rt△AEF中,EF=
.
∴异面直线AB和CD之间的距离为
.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
如图空间四边形ABCD中，AC=4，BD=2，E，F分别是BC和AD的中点．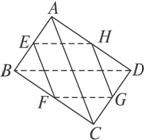
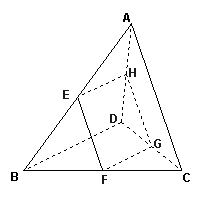(历史方向) 如图,空间四边形ABCD中,AC,BD为对角线,E,F分别为AB,BC的中点,G,H分别在边CD,DA上,且
.
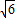，求AC与BD所成角的余弦值．