题目内容
已知幂函数 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数
上是单调增函数
(1)求函数 的解析式;
的解析式;
(2)设函数 ,其中
,其中 .若函数
.若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据函数的单调性分析出指数大于零,解不等式可得 的取值范围,再利用
的取值范围,再利用 得
得 ,然后根据幂函数
,然后根据幂函数 为偶函数可得
为偶函数可得 ;(2)根据导数求极值,为使方程
;(2)根据导数求极值,为使方程 只有
只有 一个根,则必须
一个根,则必须 恒成立,于是根据判别式可求.
恒成立,于是根据判别式可求.
试题解析:(1) 在区间
在区间 上是单调增函数,
上是单调增函数,
即
 又
又 4分
4分
而 时,
时, 不是偶函数,
不是偶函数, 时,
时, 是偶函数,
是偶函数,
 .
6分
.
6分
(2) 显然
显然 不是方程
不是方程 的根.
的根.
为使 仅在
仅在 处有极值,必须
处有极值,必须 恒成立, 8分
恒成立, 8分
即有 ,解不等式,得
,解不等式,得 .
11分
.
11分
这时, 是唯一极值.
是唯一极值. 
 .
12分
.
12分
考点:1.幂函数;2.函数的单调性;3.导数公式;4.函数的极值.

练习册系列答案
相关题目
 为偶函数,且在区间(0,+∞)上是单调递减函数.
为偶函数,且在区间(0,+∞)上是单调递减函数. 的奇偶性.
的奇偶性.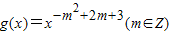 为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.
为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.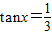 ,求F(x)的值;
,求F(x)的值;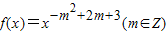 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数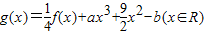 ,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.
,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围. 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数 ,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.
,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围. 为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数
为偶函数且在区间(0,+∞)上是单调递减函数。(1)求函数f(x)的解析式;(2)讨论函数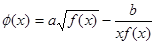 的奇偶性。(10分)
的奇偶性。(10分)