Question

如图，三棱柱ABC-A₁B₁C₁的所有棱长均等于1，且∠A₁AB=∠A₁AC=60°，则该三棱柱的体积是______．

Answer 1

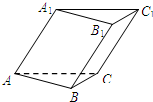
由于三棱柱ABC-A₁B₁C₁的所有棱长均等于1，且∠A₁AB=∠A₁AC=60°，
所以点A₁在底面内的投影点O必定在底部正三角形ABC的∠BAC的角平分线上，
有公式cosA₁AB=cos∠A₁AO×cos∠OAB?cos60°=cos∠A₁AO×cos30°?cos∠A1AO=

cos60°

cos30°

=

3

3

，sin∠A1AO=

6

3

，在直角三角形A₁A0中：A1O=

6

3

，所以该柱体的体积为：

1

2

× 1×1×sin60°×

6

3

=

2

4

．
故答案为：

2

4

．