题目内容
四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作,要求每所学校至少有一名专家.
(1)求评估小组中甲、乙两名专家不在同一所学校的概率;
(2)设随机变量ξ为这五名专家到A校评估的人数,求ξ的分布列与数学期望Eξ.
(1)求评估小组中甲、乙两名专家不在同一所学校的概率;
(2)设随机变量ξ为这五名专家到A校评估的人数,求ξ的分布列与数学期望Eξ.
分析:(1)先求出评估小组中甲、乙两名专家被分配在同一所学校的概率,由此能求出甲、乙两名专家不在同一所学校的概率.
(2)随机变量ξ的可能取值为1,2,分别求出P(ξ=2),P(ξ=1),由此能求出ξ的分布列的ξ的数学期望Eξ.
(2)随机变量ξ的可能取值为1,2,分别求出P(ξ=2),P(ξ=1),由此能求出ξ的分布列的ξ的数学期望Eξ.
解答:解:(1)记评估小组中甲、乙两名专家被分配在同一所学校的事件为F,
那么P(F)=
=
,…(3分)
所以甲、乙两名专家不在同一所学校的概率为:
P(
)=1-P(F)=
.…(5分)
(2)随机变量ξ的可能取值为1,2,
则P(ξ=2)=
=
;
P(ξ=1)=1-P(ξ=2)=
.…(9分)
所以ξ的分布列是:
所以ξ的数学期望Eξ=1×
+2×
=
.…(13分)
那么P(F)=
| ||||
|
| 1 |
| 10 |
所以甲、乙两名专家不在同一所学校的概率为:
P(
. |
| F |
| 9 |
| 10 |
(2)随机变量ξ的可能取值为1,2,
则P(ξ=2)=
| ||||
|
| 1 |
| 4 |
P(ξ=1)=1-P(ξ=2)=
| 3 |
| 4 |
所以ξ的分布列是:
| ξ | 1 | 2 | ||||
| P |
|
|
| 3 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
点评:本题考查离散型随机变量的分布列和数学期望,是中档题.解题时要认真审题,仔细解答,注意概率知识的合理运用.

练习册系列答案
相关题目
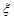 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求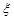 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求