Question

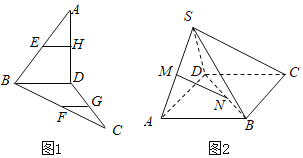
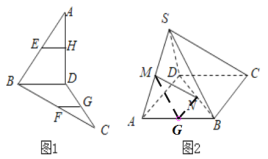
【题目】（1）如图（1）已知E，F，G，H为空间四边形ABCD的边AB，BC，CD，DA上的点，且EHFG．求证：EHBD．

（2）如图（2）：S是平行四边形ABCD平面外一点，M，N分别是SA，BD上的点，且，求证：MN平面SBC．

Answer 1

【答案】（1）见解析 （2）见解析

【解析】

（1）先证明EH平面BCD，再利用线面平行的性质即可得证；

（2）过N作NGAD，交AB于G，证明MG平面SBC、NG平面SBC后即可证明平面SBC平面MNG，即可得证.

（1）证明：如图（1），E，F，G，H为空间四边形ABCD的边AB，BC，CD，DA上的点，

∵EHFG，EH平面BCD，FG平面BCD，

∴EH平面BCD，

∵平面ABD∩平面BCD＝BD，∴BD平面ABD，

∵EH平面ABD，∴EHBD．

（2）证明：如图（2），S是平行四边形ABCD平面外一点，

过N作NGAD，交AB于G，连接MG，可得，

由已知条件，得，∴MGSB．

∵MG平面SBC，SB平面SBC，∴MG平面SBC．

又ADBC，∴NGBC，

∵NG平面SBC，BC平面SBC

∴NG平面SBC，NG∩MG＝G，

∴平面SBC平面MNG，

∵MN平面MNG，∴MN平面SBC．