题目内容
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC的中点,G为AC上一点.
(Ⅰ)求证:BD⊥FG;
(Ⅱ)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由.
(Ⅰ)求证:BD⊥FG;
(Ⅱ)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由.
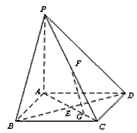
(Ⅰ)证明:∵PA⊥面ABCD,四边形ABCD是正方形,其对角线BD、AC交于点E,
∴PA⊥BD,AC⊥BD,
∴BD⊥平面APC,
∵ 平面PAC,
平面PAC,
∴BD⊥FG。
(Ⅱ)解:当G为EC的中点,即 时,FG∥平面PBD,
时,FG∥平面PBD,
理由如下:连结PE,由F为PC的中点,G为EC的中点,知FG∥PE,
而 平面PBD,
平面PBD, 平面PBD,
平面PBD,
故FG∥平面PBD。
∴PA⊥BD,AC⊥BD,
∴BD⊥平面APC,
∵
 平面PAC,
平面PAC,∴BD⊥FG。
(Ⅱ)解:当G为EC的中点,即
 时,FG∥平面PBD,
时,FG∥平面PBD,理由如下:连结PE,由F为PC的中点,G为EC的中点,知FG∥PE,
而
 平面PBD,
平面PBD, 平面PBD,
平面PBD,故FG∥平面PBD。

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
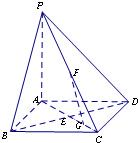 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.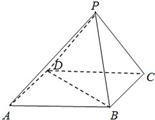 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.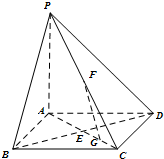 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.