题目内容
 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.(Ⅰ)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(Ⅱ)当二面角B-PC-D的大小为
| 2π | 3 |
分析:(Ⅰ)要使FG∥平面PBD,只需FG∥EP,以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,建立空间直角坐标系A-xyz如图所示,设G点坐标为(m,m,0),根据向量平行的充要条件,可得变量m的值,进而可得点G在线段AC上的位置.
(II)分别求出平面PBC的一个法向量和平面PDC的一个法向量,进而根据二面角B-PC-D的大小为
,可得变量a值,进而根据∠PCA就是PC与底面ABCD所成的角,可得PC与底面ABCD所成角的正切值.
(II)分别求出平面PBC的一个法向量和平面PDC的一个法向量,进而根据二面角B-PC-D的大小为
| 2π |
| 3 |
解答: 解:(Ⅰ)以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,
解:(Ⅰ)以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,
建立空间直角坐标系A-xyz如图所示,
设正方形ABCD的边长为1,PA=a,则
A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E(
,
,0),F(
,
,
),G(m,m,0)(0<m<
).
要使FG∥平面PBD,只需FG∥EP,
而
=(
,
,-a),
由
=λ
可得
解得λ=
,m=
,
∴G点坐标为(
,
,0)
∴
=
,
故当AG=
AC时,FG∥平面PBD.
(Ⅱ)设平面PBC的一个法向量为
=(x,y,z),
则
而
=(1,1,-a),
=(0,1,0),
∴
取z=1,得
=(a,0,1),
同理可得平面PDC的一个法向量
=(0,a,1),
设u,v所成的角为θ,
则|cosθ|=|cos
|=
,
即
=
,
∴
=
,
∴a=1,
∵PA⊥面ABCD,
∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA=
=
=
.
 解:(Ⅰ)以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,
解:(Ⅰ)以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,建立空间直角坐标系A-xyz如图所示,
设正方形ABCD的边长为1,PA=a,则
A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 2 |
要使FG∥平面PBD,只需FG∥EP,
而
| PE |
| 1 |
| 2 |
| 1 |
| 2 |
由
| FG |
| PE |
|
解得λ=
| 1 |
| 2 |
| 3 |
| 4 |
∴G点坐标为(
| 3 |
| 4 |
| 3 |
| 4 |
∴
| AG |
| 3 |
| 4 |
| AC |
故当AG=
| 3 |
| 4 |
(Ⅱ)设平面PBC的一个法向量为
| u |
则
|
而
| PC |
| BC |
∴
|
取z=1,得
| u |
同理可得平面PDC的一个法向量
| v |
设u,v所成的角为θ,
则|cosθ|=|cos
| 2π |
| 3 |
| 1 |
| 2 |
即
| |u•v| |
| |u||v| |
| 1 |
| 2 |
∴
| 1 | ||||
|
| 1 |
| 2 |
∴a=1,
∵PA⊥面ABCD,
∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA=
| PA |
| AC |
| 1 | ||
|
| ||
| 2 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的判断,其中建立空间坐标系,将直线与平面的关系,及二面角问题转化为向量问题是解答的关键.

练习册系列答案
相关题目
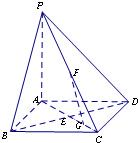 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.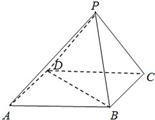 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.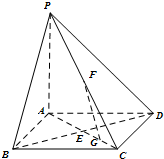 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.