题目内容
13.将函数f(x)=$\sqrt{-{x}^{2}+2x+3}$-$\sqrt{3}$(x∈[0,2])的图象绕坐标原点逆时针旋转θ (θ为锐角),若所得曲线仍是函数的图象,则θ的最大值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
分析 作出f(x)的函数图象,求出f(x)在x=0处的切线的倾斜角α,即可得出θ的最大值.
解答 解:作出f(x)的函数图象如图所示:
设f(x)在x=0处的切线方程为y=kx,则k=f′(0),
∵f′(x)=$\frac{1}{2}$(-x2+2x+3)${\;}^{-\frac{1}{2}}$•(-2x+2),∴k=f′(0)=$\frac{\sqrt{3}}{3}$,
∴切线的倾斜角α=$\frac{π}{6}$,
∴θ的最大值为$\frac{π}{2}-\frac{π}{6}$=$\frac{π}{3}$.
故选C.
点评 本题考查了函数的概念,导数的几何意义,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.在区间[-1,0]上任取两实数x、y,则y<3x的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
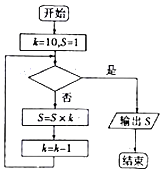 执行如图所示的储蓄框图,若输出S的值为720,则判断框内可填入的条件是k≤7?.
执行如图所示的储蓄框图,若输出S的值为720,则判断框内可填入的条件是k≤7?.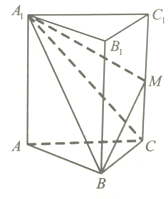 如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.
如图,在直三棱柱中ABC-A1B1C1中,二面角A-A1B-C是直二面角,AB=BC═2,点M是棱CC1的中点,三棱锥M-BCA1的体积为1.