题目内容
在长度为3的线段AB上任取一点C，那么线段AC的长度小于2的概率 ．
考点：几何概型
专题：概率与统计
分析：由题意可得，属于与区间长度有关的几何概率模型，试验的全部区域长度为3，基本事件的区域长度为2，代入几何概率公式可求．
解答：
解：AB的区间长度为3，
“线段AC的长度小于2”为事件 A，则满足A的区间长度为2，
据几何概率的计算公式可得，P（A）=
．
故答案为：
“线段AC的长度小于2”为事件 A，则满足A的区间长度为2，
据几何概率的计算公式可得，P（A）=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题主要考查了几何概型，解答的关键是将原问题转化为几何概型问题后应用几何概率的计算公式求解．
练习册系列答案
相关题目
若复数z=
，则z为（ ）
| 1-i |
| 1+i |
| A、i | B、-i | C、2i | D、1+i |
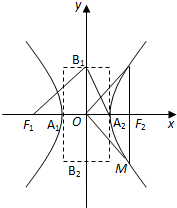我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac，则该双曲线是黄金双曲线；
③若∠F1B1A2=90°，则该双曲线是黄金双曲线；
④若∠MON=90°，则该双曲线是黄金双曲线．
| A、①② | B、①③ |
| C、①③④ | D、①②③④ |
执行如图所示的程序框图，如果输入a=2，b=2，那么输出的a值为（ ）
| A、14 | B、15 | C、16 | D、17 |
下列命题中，为真命题的是（ ）
A、?x∈[
| ||
| B、?x∈R，x2＜x3 | ||
C、?x∈(0，
| ||
| D、?x∈R，x2+x=-1 |
已知过两点A（-1，1），B（4，a）的直线斜率为1，那么a的值是（ ）
| A、-6 | B、-4 | C、4 | D、6 |
设x，y满足约束条件
（ ）
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|
已知x∈R，则“x＞1”是“x2＞x”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |