Question

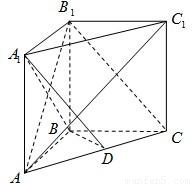
如图，在直三棱柱ABC-A₁B₁C₁中，AB=BB₁，AC₁⊥A₁B，D为AC的中点．
（Ⅰ）求证：B₁C∥平面A₁BD；
（Ⅱ）求证：平面AB₁C₁⊥平面ABB₁A₁．

Answer 1

【答案】分析：（Ⅰ）设AB₁∩A₁B=O，连接OD，利用直线OD与直线B₁C平行，来推导出B₁C∥平面A₁BD．
（Ⅱ）由AB=BB₁得ABB₁A₁正方形⇒A₁B⊥AB₁，再由A₁B⊥AC₁⇒A₁B⊥平面AB₁C₁⇒平面AB₁C₁⊥平面ABB₁A₁．
解答：解：（Ⅰ）设AB₁∩A₁B=O，连接OD．
由于点O是AB₁的中点，又D为AC的中点，所以OD∥B₁C（5分）
而B₁C?平面A₁BD，OD?平面A₁BD，所以B₁C∥平面A₁BD（7分）
（Ⅱ）因为AB=BB₁，所以是ABB₁A₁正方形，则A₁B⊥AB₁，
又A₁B⊥AC₁，且AC₁，AB₁?平面AB₁C₁，AC₁∩AB₁=A，所以A₁B⊥平面AB₁C₁（12分）
而A₁B?平面ABB₁A₁，所以平面AB₁C₁⊥平面ABB₁A₁（14分）
点评：本题考查平面和平面垂直的判定和性质以及线面平行的判定．在证明线面平行时，其常用方法时转化为线线平行或面面平行．