题目内容
设椭圆C: 的一个顶点与抛物线:
的一个顶点与抛物线: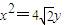 的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率
的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率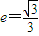 ,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.(I)求椭圆C的方程;
(Ⅱ)是否存在直线l,使得
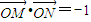 ,若存在,求出直线l的方程;若不存在,说明理由;
,若存在,求出直线l的方程;若不存在,说明理由;(Ⅲ)若AB是椭圆C经过原点O的弦,MN∥AB,求
 的值.
的值.
【答案】分析:(I)根据抛物线方程得它的焦点坐标为(0, ),即为椭圆的上顶点,得到b=
),即为椭圆的上顶点,得到b= ,结合椭圆的离心率为
,结合椭圆的离心率为 ,可解出a、c的值,即可得到椭圆C的方程;
,可解出a、c的值,即可得到椭圆C的方程;
(II)设M(x1,y1),N(x2,y2),直线l方程:y=k(x-1),与椭圆消去y得关于x的方程,由根与系数关系得:x1+x2= ,x1x2=
,x1x2= ,代入
,代入 =x1x2+y1y2的式子并进行化简,可得当k=
=x1x2+y1y2的式子并进行化简,可得当k= 时,
时, ,从而得到符合题意的直线l方程;
,从而得到符合题意的直线l方程;
(III)设M(x1,y1),N(x2,y2),利用(II)的方程并结合两点距离公式进行化简,可得|MN|= ,再设A(x3,y3),B(x4,y4),同样的方程可得|AB|=2
,再设A(x3,y3),B(x4,y4),同样的方程可得|AB|=2 ,由此代入
,由此代入 化简,即可得到要求的值.
化简,即可得到要求的值.
解答:解:(I)抛物线 的焦点坐标为(0,
的焦点坐标为(0, ),可得椭圆的上顶点为(0,
),可得椭圆的上顶点为(0, ),得b=
),得b=
∵椭圆的离心率 ,得
,得 =
= ,解得a=
,解得a= ,c=1
,c=1
∴椭圆C的方程是
(II)由(I)得椭圆C的右焦点为F2(1,0)
①当直线l与x轴垂直时,直线l斜率不存在,此时M(1, ),N(1,-
),N(1,- )
)
∴ =1×1+
=1×1+ ×(-
×(- )=-
)=- ,不符合题意;
,不符合题意;
②当直线l与x轴不垂直时,设直线方程l:y=k(x-1),且M(x1,y1),N(x2,y2)
由 ,得(2+3k2)x2-6k2x+3k2-6=0
,得(2+3k2)x2-6k2x+3k2-6=0
x1+x2= ,x1•x2=
,x1•x2=
∴ =x1•x2+y1•y2=x1•x2+k2[x1•x2-(x1+x2)+1]=(1+k2)x1•x2-k2(x1+x2)+k2=-1
=x1•x2+y1•y2=x1•x2+k2[x1•x2-(x1+x2)+1]=(1+k2)x1•x2-k2(x1+x2)+k2=-1
即(1+k2)• -k2•
-k2• +k2=-1
+k2=-1
解之得k= ,故直线l的方程是y=
,故直线l的方程是y= (x-1)或y=-
(x-1)或y=- (x-1).
(x-1).
(III)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(II)得|MN|= =
= |x1-x2|
|x1-x2|
= =
= =
=
由 消去y,整理得
消去y,整理得
∴|AB|= =
= |x3-x4|=2
|x3-x4|=2
∴ =
= =6.
=6.
点评:本题给出椭圆的上顶点与抛物线的焦点重合,求椭圆方程并求满足数量积 的焦点弦所在直线方程,着重考查了椭圆、抛物线的简单性质,直线与圆锥曲线关系和向量的数量积等知识,属于中档题.
的焦点弦所在直线方程,着重考查了椭圆、抛物线的简单性质,直线与圆锥曲线关系和向量的数量积等知识,属于中档题.
 ),即为椭圆的上顶点,得到b=
),即为椭圆的上顶点,得到b= ,结合椭圆的离心率为
,结合椭圆的离心率为 ,可解出a、c的值,即可得到椭圆C的方程;
,可解出a、c的值,即可得到椭圆C的方程;(II)设M(x1,y1),N(x2,y2),直线l方程:y=k(x-1),与椭圆消去y得关于x的方程,由根与系数关系得:x1+x2=
 ,x1x2=
,x1x2= ,代入
,代入 =x1x2+y1y2的式子并进行化简,可得当k=
=x1x2+y1y2的式子并进行化简,可得当k= 时,
时, ,从而得到符合题意的直线l方程;
,从而得到符合题意的直线l方程;(III)设M(x1,y1),N(x2,y2),利用(II)的方程并结合两点距离公式进行化简,可得|MN|=
 ,再设A(x3,y3),B(x4,y4),同样的方程可得|AB|=2
,再设A(x3,y3),B(x4,y4),同样的方程可得|AB|=2 ,由此代入
,由此代入 化简,即可得到要求的值.
化简,即可得到要求的值.解答:解:(I)抛物线
 的焦点坐标为(0,
的焦点坐标为(0, ),可得椭圆的上顶点为(0,
),可得椭圆的上顶点为(0, ),得b=
),得b=
∵椭圆的离心率
 ,得
,得 =
= ,解得a=
,解得a= ,c=1
,c=1∴椭圆C的方程是

(II)由(I)得椭圆C的右焦点为F2(1,0)
①当直线l与x轴垂直时,直线l斜率不存在,此时M(1,
 ),N(1,-
),N(1,- )
)∴
 =1×1+
=1×1+ ×(-
×(- )=-
)=- ,不符合题意;
,不符合题意;②当直线l与x轴不垂直时,设直线方程l:y=k(x-1),且M(x1,y1),N(x2,y2)
由
 ,得(2+3k2)x2-6k2x+3k2-6=0
,得(2+3k2)x2-6k2x+3k2-6=0x1+x2=
 ,x1•x2=
,x1•x2=
∴
 =x1•x2+y1•y2=x1•x2+k2[x1•x2-(x1+x2)+1]=(1+k2)x1•x2-k2(x1+x2)+k2=-1
=x1•x2+y1•y2=x1•x2+k2[x1•x2-(x1+x2)+1]=(1+k2)x1•x2-k2(x1+x2)+k2=-1即(1+k2)•
 -k2•
-k2• +k2=-1
+k2=-1解之得k=
 ,故直线l的方程是y=
,故直线l的方程是y= (x-1)或y=-
(x-1)或y=- (x-1).
(x-1).(III)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(II)得|MN|=
 =
= |x1-x2|
|x1-x2|=
 =
= =
=
由
 消去y,整理得
消去y,整理得
∴|AB|=
 =
= |x3-x4|=2
|x3-x4|=2
∴
 =
= =6.
=6.点评:本题给出椭圆的上顶点与抛物线的焦点重合,求椭圆方程并求满足数量积
 的焦点弦所在直线方程,着重考查了椭圆、抛物线的简单性质,直线与圆锥曲线关系和向量的数量积等知识,属于中档题.
的焦点弦所在直线方程,着重考查了椭圆、抛物线的简单性质,直线与圆锥曲线关系和向量的数量积等知识,属于中档题. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的一个顶点与抛物线C2:
的一个顶点与抛物线C2: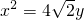 的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率
的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率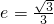 ,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.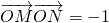 ,若存在,求出直线l的方程;若不存在,说明理由.
,若存在,求出直线l的方程;若不存在,说明理由. 的一个顶点与抛物线:
的一个顶点与抛物线: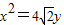 的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率
的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率 ,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.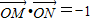 ,若存在,求出直线l的方程;若不存在,说明理由;
,若存在,求出直线l的方程;若不存在,说明理由;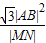 的值.
的值.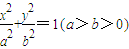 的一个顶点与抛物线C2:
的一个顶点与抛物线C2: 的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率
的焦点重合,F1、F2分别是椭圆的左、右焦点,离心率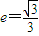 ,过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
,过椭圆右焦点F2的直线l与椭圆C交于M、N两点. ,若存在,求出直线l的方程;若不存在,说明理由.
,若存在,求出直线l的方程;若不存在,说明理由.