题目内容
有甲、乙等7名选手参加一次演讲比赛，采用抽签的方式随机确定每名选手的演出顺序（序号为1，2，…，7）.
（Ⅰ）甲选手的演出序号是1的概率；
（Ⅱ）求甲、乙两名选手的演出序号至少有一个为奇数的概率；
（Ⅲ）设在甲、乙两名选手之间的演讲选手个数为
,求的分布列与期望.
【答案】
解：（Ⅰ）设
表示“甲选手的演出序号是1”，所以
所以甲选手的演出序号是1的概率为
………………………… 3分
（Ⅱ）设
表示“甲、乙两名选手的演出序号至少有一个为奇数”，
表示“甲、乙两名选手的演出序号都是偶数”. 所以
所以甲、乙两名选手的演出序号至少有一个为奇数的概率为
……………………… 6分
（Ⅲ）
的可能取值为
，
，
，
，
，
，
……………………… 7分
所以
，
，
，
，
，
.……………10分
所以的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
………………… 12分
所以
………………… 13分
【解析】略
练习册系列答案
阅读快车系列答案
相关题目
的分布列与期望。
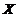,求