题目内容
有甲、乙等7名选手参加一次演讲比赛,采用抽签的方式随机确定每名选手的演出顺序(序号为1,2,…,7).
(Ⅰ)甲选手的演出序号是1的概率;
(Ⅱ)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(Ⅲ)设在甲、乙两名选手之间的演讲选手个数为X,求X的分布列与期望.
(Ⅰ)甲选手的演出序号是1的概率;
(Ⅱ)求甲、乙两名选手的演出序号至少有一个为奇数的概率;
(Ⅲ)设在甲、乙两名选手之间的演讲选手个数为X,求X的分布列与期望.
分析:(Ⅰ)设A表示“甲选手的演出序号是1”,所以P(A)=
.由此能求出甲选手的演出序号是1的概率.
(Ⅱ)设B表示“甲、乙两名选手的演出序号至少有一个为奇数”,
表示“甲、乙两名选手的演出序号都是偶数”.利用间接法能求出甲、乙两名选手的演出序号至少有一个为奇数的概率.
(Ⅲ)X的可能取值为0,1,2,3,4,5,分别求出其对应的概率,由此能求出X的分布列和期望.
| 1 |
| 7 |
(Ⅱ)设B表示“甲、乙两名选手的演出序号至少有一个为奇数”,
. |
| B |
(Ⅲ)X的可能取值为0,1,2,3,4,5,分别求出其对应的概率,由此能求出X的分布列和期望.
解答:解:(Ⅰ)设A表示“甲选手的演出序号是1”,所以P(A)=
.
所以甲选手的演出序号是1的概率为
.…(3分)
(Ⅱ)设B表示“甲、乙两名选手的演出序号至少有一个为奇数”,
表示“甲、乙两名选手的演出序号都是偶数”.
所以P(B)=1-P(
)=1-
=
.
所以甲、乙两名选手的演出序号至少有一个为奇数的概率为
.…(6分)
(Ⅲ)X的可能取值为0,1,2,3,4,5,…(7分)
所以P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
P(X=4)=
=
,
P(X=5)=
=
.…(10分)
所以X的分布列为
…(12分)
所以EX=0×
+1×
+2×
+3×
+4×
+5×
=
.…(13分)
| 1 |
| 7 |
所以甲选手的演出序号是1的概率为
| 1 |
| 7 |
(Ⅱ)设B表示“甲、乙两名选手的演出序号至少有一个为奇数”,
. |
| B |
所以P(B)=1-P(
. |
| B |
| ||
|
| 6 |
| 7 |
所以甲、乙两名选手的演出序号至少有一个为奇数的概率为
| 6 |
| 7 |
(Ⅲ)X的可能取值为0,1,2,3,4,5,…(7分)
所以P(X=0)=
| 12 | ||
|
| 2 |
| 7 |
P(X=1)=
| 10 | ||
|
| 5 |
| 21 |
P(X=2)=
| 8 | ||
|
| 4 |
| 21 |
P(X=3)=
| 6 | ||
|
| 1 |
| 7 |
P(X=4)=
| 4 | ||
|
| 2 |
| 21 |
P(X=5)=
| 2 | ||
|
| 1 |
| 21 |
所以X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
所以EX=0×
| 2 |
| 7 |
| 5 |
| 21 |
| 4 |
| 21 |
| 1 |
| 7 |
| 2 |
| 21 |
| 1 |
| 21 |
| 5 |
| 3 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是历年高考拨考题型.解题时要认真审题,注意概率知识的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,求
,求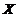 ,求
,求