题目内容
设函数f(x)=|x2-4x-5|.(1)在区间[-2,6]上画出函数f(x)的图象;
(2)设集合A={x|f(x)≥5},?B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系(要写出判断过程);
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
【答案】分析:(1)当x2-4x-5>0时,f(x)=x2-4x-5;当x2-4x-5<0时,f(x)=x2-4x-5,进而画出图象.
(2)先求出f(x)≥5的解集,再判断集合A和B的关系.
(3)设函数g(x)=kx+3k-f(x),只要证明g(x)>0恒成立即可.
解答: 解:(1)设-2≤x≤6,当x2-4x-5≥0时,
解:(1)设-2≤x≤6,当x2-4x-5≥0时,
即6≥x≥5或-1≥x≥-2时,f(x)=x2-4x-5=(x-2)2-9
当x2-4x-5<0时,即-1<x<5时,f(x)=-(x2-4x-5)=-(x-2)2+9
故作图如下.
(2)方程f(x)=5的解分别是
和 ,由于f(x)在(-∞,-1]和[2,5]上单调递减,
,由于f(x)在(-∞,-1]和[2,5]上单调递减,
在[-1,2]和[5,+∞)上单调递增,
∴ .
.
由于2+ <6,2-
<6,2-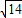 >-2
>-2
∴B?A.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)= ,
,
∵k>2,∴? .又-1≤x≤5,
.又-1≤x≤5,
①当 ,即2<k≤6时,
,即2<k≤6时,
取 ,g(x)min=
,g(x)min= .
.
∵?16≤(k-10)2<64,?
∴?(k-10)2-64<0,则g(x)min>0.
②当 ,即k>6时,取x=-1,g(x)min=2k>0.
,即k>6时,取x=-1,g(x)min=2k>0.
由①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
点评:本题主要考查了函数图象的应用.注意数形结合.
(2)先求出f(x)≥5的解集,再判断集合A和B的关系.
(3)设函数g(x)=kx+3k-f(x),只要证明g(x)>0恒成立即可.
解答:
 解:(1)设-2≤x≤6,当x2-4x-5≥0时,
解:(1)设-2≤x≤6,当x2-4x-5≥0时,即6≥x≥5或-1≥x≥-2时,f(x)=x2-4x-5=(x-2)2-9
当x2-4x-5<0时,即-1<x<5时,f(x)=-(x2-4x-5)=-(x-2)2+9
故作图如下.
(2)方程f(x)=5的解分别是

和
 ,由于f(x)在(-∞,-1]和[2,5]上单调递减,
,由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,
∴
 .
.由于2+
 <6,2-
<6,2-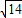 >-2
>-2∴B?A.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)=
 ,
,∵k>2,∴?
 .又-1≤x≤5,
.又-1≤x≤5,①当
 ,即2<k≤6时,
,即2<k≤6时,取
 ,g(x)min=
,g(x)min= .
.∵?16≤(k-10)2<64,?
∴?(k-10)2-64<0,则g(x)min>0.
②当
 ,即k>6时,取x=-1,g(x)min=2k>0.
,即k>6时,取x=-1,g(x)min=2k>0.由①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
点评:本题主要考查了函数图象的应用.注意数形结合.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|