题目内容

设函数f（x）=msinx+cosx（x∈R）的图象经过点(
π
2
，1)．
（1）求f（x）的解析式，并求函数的最小正周期．
（2）若f(α+
π
4
)=
3
2
5
且α∈(0，
π
2
)，求f(2α-
π
4
)的值．
分析：（1）由题意可得m=1，进而可得函数解析式，可得周期；（2）由（1）化简已知可得cosα=
3
5
，进而可得sinα的值，而要求的值可化为2
2
sinαcosα，代值即可．
解答：解：（1）∵函数f（x）=msinx+cosx（x∈R）的图象经过点(
π
2
，1)
∴msin
π
2
+cos
π
2
=1，∴m=1…．（2分）
∴f(x)=sinx+cosx=
2
sin(x+
π
4
)…．（3分）
∴函数的最小正周期T=2π…（4分）
（2）由（1）知：f(α+
π
4
)=
2
sin(α+
π
4
+
π
4
)=
2
sin(α+
π
2
)=
2
cosα=
3
2
5
…（6分）
∴cosα=
3
5
，又因为α∈(0，
π
2
)∴sinα=
1-cos2α
=
4
5
…（9分）
∴f(2α-
π
4
)=
2
sin(2α-
π
4
+
π
4
)=
2
sin2α=2
2
sinαcosα=
24
2
25
…（12分）
点评：本题为三角函数的运算，涉及两角和与差的公式以及三角函数的图象，属基础题．
练习册系列答案
相关题目
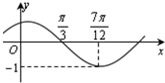精英家教网已知函数f（x）=Msin（ωx+φ）（其中M＞0，ω＞0，|φ|＜
π
2
）的图象如图所示．
（1）求函数f（x）的表达式；
（2）设α∈(
π
6
，  
2π
3
)，  β∈(-
5π
6
，-
π
3
)，  f(
α
2
)=
3
5
，  f(
β
2
)=-
4
5
，求cos2（α-β）的值．
设函数f（x）=x2013+x，x∈R，若当θ∈[0 ， 
π2
)时，f（msinθ）+f（1-m）＞0恒成立，则m的取值范围是
（-∞，1）
（-∞，1）
．
设函数f（x）=x3+x，x∈R．若当0＜θ＜
π
2
时，不等式f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（　　）
（2013•泸州一模）已知命题p：夹角为m的单位向量a，b使|a-b|＞l，命题q：函数f（x）=msin（mx）的导函数为f′（x），若?xo∈R，f′(xo)≥
4π25
．设符合p∧q为真的实数m的取值的集合为A．
（I）求集合A；
（Ⅱ）若B={x∈R|x2=πa}，且B∩A=∅，求实数a的取值范围．
设?＞0，m＞0，若函数f（x）=msin
ωx
2
cos
ωx
2
在区间(-
π
3
，
π
4
)上单调递增，则ω的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网