题目内容
已知椭圆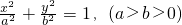 的离心率为
的离心率为 ,点P(2,1)是椭圆上一定点,若斜率为
,点P(2,1)是椭圆上一定点,若斜率为 的直线与椭圆交于不同的两点A、B.
的直线与椭圆交于不同的两点A、B.
( I)求椭圆方程;
( II)求△PAB面积的最大值.
解:( I)∵ ,
,
∴ ,
,
又P(2,1)在椭圆上,代入椭圆方程,
得: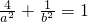 ,
,
∴a2=8,b2=2,
椭圆方程为: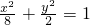 …(6分)
…(6分)
( II)设直线AB的方程为: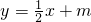 ,
,
与椭圆联列方程组得, ,
,
代入得:2x2+4mx+4m2-8=0,…(8分)
∵△=16m2-8(4m2-8)>0,
解得,-2<m<2
由韦达定理得:x1+x2=-2m,
x1x2=2m2-4 =
=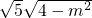
P到直线AB的距离: ,…(12分)
,…(12分)

当4-m2=m2,
即 时,
时,
S△PAB有最大值2 …(15分)
分析:( I)由 ,知
,知 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
( II)设直线AB的方程为: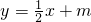 ,与椭圆联列方程组得,
,与椭圆联列方程组得, ,代入得:2x2+4mx+4m2-8=0,再由根的判别式和韦达定理能求出S△PAB的最大值.
,代入得:2x2+4mx+4m2-8=0,再由根的判别式和韦达定理能求出S△PAB的最大值.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,
,∴
 ,
,又P(2,1)在椭圆上,代入椭圆方程,
得:
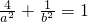 ,
,∴a2=8,b2=2,
椭圆方程为:
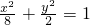 …(6分)
…(6分)( II)设直线AB的方程为:
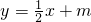 ,
,与椭圆联列方程组得,
 ,
,代入得:2x2+4mx+4m2-8=0,…(8分)
∵△=16m2-8(4m2-8)>0,
解得,-2<m<2
由韦达定理得:x1+x2=-2m,
x1x2=2m2-4
 =
=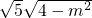
P到直线AB的距离:
 ,…(12分)
,…(12分)
当4-m2=m2,
即
 时,
时,S△PAB有最大值2 …(15分)
分析:( I)由
 ,知
,知 ,由此能求出椭圆方程.
,由此能求出椭圆方程.( II)设直线AB的方程为:
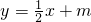 ,与椭圆联列方程组得,
,与椭圆联列方程组得, ,代入得:2x2+4mx+4m2-8=0,再由根的判别式和韦达定理能求出S△PAB的最大值.
,代入得:2x2+4mx+4m2-8=0,再由根的判别式和韦达定理能求出S△PAB的最大值.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: