题目内容
已知椭圆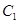 的中心在原点、焦点在
的中心在原点、焦点在 轴上,抛物线
轴上,抛物线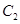 的顶点在原点、焦点在
的顶点在原点、焦点在 轴上.小明从曲线
轴上.小明从曲线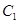 、
、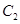 上各取若干个点(每条曲线上至少取两个点),并记录其坐标(
上各取若干个点(每条曲线上至少取两个点),并记录其坐标(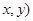 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆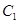 上,也不在抛物线
上,也不在抛物线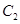 上,小明的记录如下:
上,小明的记录如下:
 | 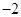 | 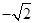 |  |  | 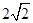 |  |
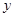 |  |  | 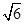 | 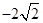 | 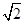 | 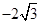 |
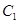 的方程为
的方程为

解析试题分析:由题意可知:点(0,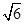 )是椭圆
)是椭圆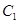 的短轴的一个端点,或点(?
的短轴的一个端点,或点(?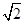 ,0)是椭圆
,0)是椭圆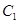 的长轴的一个端点.以下分两种情况讨论:
的长轴的一个端点.以下分两种情况讨论:
假设点(0,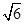 )是椭圆
)是椭圆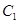 的短轴的一个端点,则
的短轴的一个端点,则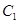 可以写成
可以写成 ,经验证可得:若点(
,经验证可得:若点(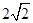 ,
,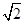 )在
)在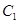 上,代入求得
上,代入求得 ,即
,即 ,剩下的4个点中(-2,2)也在此椭圆上.
,剩下的4个点中(-2,2)也在此椭圆上.
假设抛物线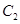 的方程为
的方程为 ,把点(2,
,把点(2,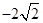 )代入求得p=2,∴
)代入求得p=2,∴ ,则点(3,
,则点(3,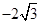 ),则只剩下一个点(
),则只剩下一个点(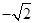 ,0)既不在椭圆上,也不在抛物线上,满足条件.
,0)既不在椭圆上,也不在抛物线上,满足条件.
假设抛物线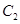 的方程为
的方程为 ,经验证不符合题意.
,经验证不符合题意.
假设点(?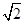 ,0)是椭圆
,0)是椭圆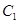 的长轴的一个端点,则
的长轴的一个端点,则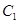 可以写成
可以写成 ,经验证不满足条件,应舍去.综上可知:可推断椭圆
,经验证不满足条件,应舍去.综上可知:可推断椭圆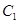 的方程为
的方程为 ,故答案为
,故答案为 .
.
考点:椭圆的简单性质.

练习册系列答案
相关题目
 中,曲线
中,曲线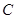 的离心率为
的离心率为 ,且过点
,且过点 ,则曲线
,则曲线 是抛物线
是抛物线 上一动点,则点
上一动点,则点 的距离与
的距离与 的距离和的最小值是 .
的距离和的最小值是 . 的焦点在直线
的焦点在直线 上,则
上,则 _____;
_____;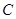 的准线方程为_____.
的准线方程为_____. 的焦点和虚轴端点,若线段FB的中点在双曲线C上,则双曲线C的离心率是___________.
的焦点和虚轴端点,若线段FB的中点在双曲线C上,则双曲线C的离心率是___________. 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为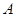 , 短轴上方端点为
, 短轴上方端点为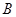 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.
 的一条渐近线的方程为
的一条渐近线的方程为 ,则
,则 =_____ __.
=_____ __. +y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.
+y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.