题目内容
设一次函数f(x)的图象关于直线y=x对称的图象为C,且f(-1)=0.若点(n+1,
)(n∈N*)在曲线C上,并且a1=a2=1.
(1)求曲线C的方程;?
(2)求数列{an}的通项公式;?
(3)设Sn=
+
+…+
,求Sn.
| an+1 |
| an |
(1)求曲线C的方程;?
(2)求数列{an}的通项公式;?
(3)设Sn=
| a1 |
| 2! |
| a2 |
| 3! |
| an |
| (n+1)! |
分析:(1)设f(x)=ax+b(a≠0),可求C的方程,然后由f(-1)=0及(2,
)在曲线C上,可求a,b
(2)由点(n+1,
)在曲线C上可得,
=n,从而利用叠乘可求an,
(3)由sn=
+
+…+
,化简后可以利用裂项可求数列的和
| a2 |
| a1 |
(2)由点(n+1,
| an+1 |
| an |
| an+1 |
| an |
(3)由sn=
| 0! |
| 2! |
| 1! |
| 3! |
| (n-1)! |
| (n+1)! |
解答:解:(1)设f(x)=ax+b(a≠0),则C的方程为y=
(x-b)
由f(-1)=0可得-a+b=0①
由(2,
)在曲线C上可得,1=
(2-b)
①②联立可得,a=b=1
曲线C的方程为y=x-1
(2)由点(n+1,
)在曲线C上可得,
=n
∴
•
…
=(n-1)!
即
=(n-1)!
∵a1=1
∴an=(n-1)!
(3)sn=
+
+…+
=
+
+…+
=1-
+
-
+…+
-
=1-
=
| 1 |
| a |
由f(-1)=0可得-a+b=0①
由(2,
| a2 |
| a1 |
| 1 |
| a |
①②联立可得,a=b=1
曲线C的方程为y=x-1
(2)由点(n+1,
| an+1 |
| an |
| an+1 |
| an |
∴
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
即
| an |
| a1 |
∵a1=1
∴an=(n-1)!
(3)sn=
| 0! |
| 2! |
| 1! |
| 3! |
| (n-1)! |
| (n+1)! |
=
| 1 |
| 2×1 |
| 1 |
| 3×2 |
| 1 |
| (n+1)n |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题主要考查了互为反函数的求解,数列的叠乘法求解数列的通项及裂项求和方法的应用

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
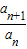 )(n∈N*)在曲线C上,并且a1=a2=1.
)(n∈N*)在曲线C上,并且a1=a2=1.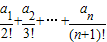 ,求Sn.
,求Sn.