题目内容
设一次函数f（x）的图象关于直线y=x对称的图象为C，且f（-1）=0．若点（n+1，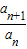
）（n∈N*）在曲线C上，并且a1=a2=1．（1）求曲线C的方程；?
（2）求数列{an}的通项公式；?
（3）设Sn=
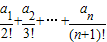，求Sn．
【答案】分析：（1）设f（x）=ax+b（a≠0），可求C的方程，然后由f（-1）=0及（2，
）在曲线C上，可求a，b
（2）由点（n+1，
）在曲线C上可得，
，从而利用叠乘可求an，
（3）由
，化简后可以利用裂项可求数列的和
解答：解：（1）设f（x）=ax+b（a≠0），则C的方程为y=
由f（-1）=0可得-a+b=0①
由（2，
）在曲线C上可得，1=
①②联立可得，a=b=1
曲线C的方程为y=x-1
（2）由点（n+1，
）在曲线C上可得，
∴
即
∵a1=1
∴an=（n-1）!
（3）
=
=
=1-
=
点评：本题主要考查了互为反函数的求解，数列的叠乘法求解数列的通项及裂项求和方法的应用
）在曲线C上，可求a，b（2）由点（n+1，
）在曲线C上可得，，从而利用叠乘可求an，（3）由
，化简后可以利用裂项可求数列的和解答：解：（1）设f（x）=ax+b（a≠0），则C的方程为y=
由f（-1）=0可得-a+b=0①
由（2，
）在曲线C上可得，1=①②联立可得，a=b=1
曲线C的方程为y=x-1
（2）由点（n+1，
）在曲线C上可得，∴
即
∵a1=1
∴an=（n-1）!
（3）
=
=
=1-
=点评：本题主要考查了互为反函数的求解，数列的叠乘法求解数列的通项及裂项求和方法的应用
练习册系列答案
备战中考寒假系列答案
相关题目