题目内容
已知函数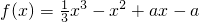 (a∈R).
(a∈R).
(1)当a=-3时,求函数f(x)的极值;
(2)设g(x)=f(x)+f′(x)+ax2,若函数g(x)在区间(-1,1)有极值,求a的取值范围;
(3)若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
解:(1)当a=-3时, ,
,
∴f'(x)=x2-2x-3=(x-3)(x+1).令f'(x)=0,得 x1=-1,x2=3.
当x<-1时,f′(x)>0,则f(x)在(-∞,-1)上单调递增;
当-1<x<3时,f′(x)<0,则f(x)在(-1,3)上单调递减;
当x>3时,f′(x)>0,f(x)在(3,+∞)上单调递增;
∴当x=-1时,f(x)取得极大值为:f(-1)= ;
;
当x=3时,f(x)取得极小值为: =-6.
=-6.
(2)∵
问题转化为方程g′(x)=0在区间(-1,1)内有解,
∴g′(-1)•g′(1)<0或
解得a<-1或a> ,
,
故a的取值范围为:(-∞,-1)∪( ,+∞).
,+∞).
(3)∵f'(x)=x2-2x+a,∴△=4-4a=4(1-a).
①若a≥1,则△≤0,∴f'(x)≥0在R上恒成立,
∴f(x)在R上单调递增.∵f(0)=-a<0,f(3)=2a>0,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
②若a<1,则△>0,
∴f'(x)=0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2=2,x1x2=a.
当x变化时,f′(x),f(x)的取值情况如下表:
∵ ,
,
∴ .∴
.∴ =
= =
= =
= ,
,
同理f(x2)= .
.
∴ =
=
= =
= .
.
令f(x1)•f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0,
故当0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).
分析:(1)当a=-3时,求出导函数f′(x)的零点,然后判断导数在零点两侧的符号,由此可得极值情况;
(2)g(x)在区间(-1,1)有极值,即g′(x)=0在(-1,1)内有解,且在解的两侧导数异号;
(3)函数f(x)的图象与x轴有且只有一个交点,即函数f(x)只有一个零点,用导数研究函数f(x)的单调性、极值,由零点存在的条件可得关于a的约束条件,由此可求其范围.
点评:本题考查函数在某点取得极值的条件,可导函数f(x)在点x0处取得极值的充要条件是f′(x0)=0,且f′(x)在x0左右两侧异号.
 ,
,∴f'(x)=x2-2x-3=(x-3)(x+1).令f'(x)=0,得 x1=-1,x2=3.
当x<-1时,f′(x)>0,则f(x)在(-∞,-1)上单调递增;
当-1<x<3时,f′(x)<0,则f(x)在(-1,3)上单调递减;
当x>3时,f′(x)>0,f(x)在(3,+∞)上单调递增;
∴当x=-1时,f(x)取得极大值为:f(-1)=
 ;
;当x=3时,f(x)取得极小值为:
 =-6.
=-6.(2)∵

问题转化为方程g′(x)=0在区间(-1,1)内有解,
∴g′(-1)•g′(1)<0或

解得a<-1或a>
 ,
,故a的取值范围为:(-∞,-1)∪(
 ,+∞).
,+∞).(3)∵f'(x)=x2-2x+a,∴△=4-4a=4(1-a).
①若a≥1,则△≤0,∴f'(x)≥0在R上恒成立,
∴f(x)在R上单调递增.∵f(0)=-a<0,f(3)=2a>0,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
②若a<1,则△>0,
∴f'(x)=0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2=2,x1x2=a.
当x变化时,f′(x),f(x)的取值情况如下表:
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 ,
,∴
 .∴
.∴ =
= =
= =
= ,
,同理f(x2)=
 .
.∴
 =
=
=
 =
= .
.令f(x1)•f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0,
故当0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).
分析:(1)当a=-3时,求出导函数f′(x)的零点,然后判断导数在零点两侧的符号,由此可得极值情况;
(2)g(x)在区间(-1,1)有极值,即g′(x)=0在(-1,1)内有解,且在解的两侧导数异号;
(3)函数f(x)的图象与x轴有且只有一个交点,即函数f(x)只有一个零点,用导数研究函数f(x)的单调性、极值,由零点存在的条件可得关于a的约束条件,由此可求其范围.
点评:本题考查函数在某点取得极值的条件,可导函数f(x)在点x0处取得极值的充要条件是f′(x0)=0,且f′(x)在x0左右两侧异号.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).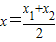 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.