题目内容
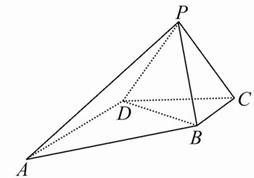
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
(1)在直线BC上是否存在一点P,使得DP 平面EAB?请证明你的结论;
平面EAB?请证明你的结论;
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
(1)在直线BC上是否存在一点P,使得DP
 平面EAB?请证明你的结论;
平面EAB?请证明你的结论;(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.

解:(1)线段BC的中点就是满足条件的点P.证明如下:
取AB的中点F连接DP、PF、EF,则FP AC,
AC, ,
,
取AC的中点M,连接EM、EC,
∵AE=AC且∠EAC=60°,
∴△EAC是正三角形,
∴EM⊥AC.
∴四边形EMCD为矩形,∴ .
.
又∵ED AC,
AC,
∴ED FP且ED=FP,
FP且ED=FP,
四边形EFPD是平行四边形.
∴DP EF,
EF,
而EF 平面EAB,DP
平面EAB,DP 平面EAB,
平面EAB,
∴DP 平面EAB.
平面EAB.
(2)过B作AC的平行线l,过C作l的垂线交l于G,连接DG,
∵ED AC,
AC,
∴ED l,l是平面EBD与平面ABC所成二面角的棱.
l,l是平面EBD与平面ABC所成二面角的棱.
∵平面EAC⊥平面ABC,DC?AC,
∴DC⊥平面ABC,
又∵l 平面ABC,∴l⊥平面DGC,
平面ABC,∴l⊥平面DGC,
∴l⊥DG,
∴∠DGC是所求二面角的平面角.
设AB=AC=AE=2a,则 ,GC=2a,
,GC=2a,
∴ ,
,
∴ .
.
取AB的中点F连接DP、PF、EF,则FP
 AC,
AC, ,
,取AC的中点M,连接EM、EC,
∵AE=AC且∠EAC=60°,
∴△EAC是正三角形,
∴EM⊥AC.
∴四边形EMCD为矩形,∴
 .
.又∵ED
 AC,
AC,∴ED
 FP且ED=FP,
FP且ED=FP,四边形EFPD是平行四边形.
∴DP
 EF,
EF,而EF
 平面EAB,DP
平面EAB,DP 平面EAB,
平面EAB,∴DP
 平面EAB.
平面EAB.(2)过B作AC的平行线l,过C作l的垂线交l于G,连接DG,
∵ED
 AC,
AC,∴ED
 l,l是平面EBD与平面ABC所成二面角的棱.
l,l是平面EBD与平面ABC所成二面角的棱.∵平面EAC⊥平面ABC,DC?AC,
∴DC⊥平面ABC,
又∵l
 平面ABC,∴l⊥平面DGC,
平面ABC,∴l⊥平面DGC,∴l⊥DG,
∴∠DGC是所求二面角的平面角.
设AB=AC=AE=2a,则
 ,GC=2a,
,GC=2a,∴
 ,
,∴
 .
.

练习册系列答案
相关题目
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.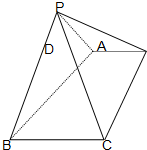 如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.
如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD. 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=