题目内容
(本小题满分12分)
已知各项均为正数的数列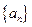 满足
满足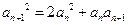 , 且
, 且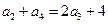 ,
,
其中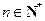 .
.
(I)求数列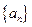 的通项公式;
的通项公式;
(II)设 数列
数列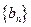 的前
的前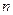 项和为
项和为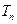 ,令
,令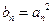 ,其中
,其中 ,试比较
,试比较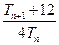 与
与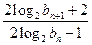 的大小,并加以证明.
的大小,并加以证明.
已知各项均为正数的数列
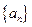 满足
满足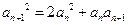 , 且
, 且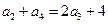 ,
,其中
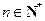 .
.(I)求数列
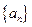 的通项公式;
的通项公式;(II)设
 数列
数列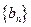 的前
的前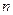 项和为
项和为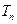 ,令
,令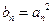 ,其中
,其中 ,试比较
,试比较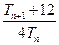 与
与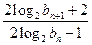 的大小,并加以证明.
的大小,并加以证明.解:(Ⅰ)因为

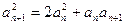 ,即
,即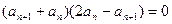
又
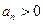 ,所以有
,所以有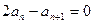 ,所以
,所以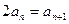
所以数列
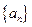 是公比为
是公比为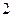 的等比数列. …………………………………………3分
的等比数列. …………………………………………3分由
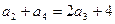 得
得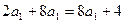 , 解得
, 解得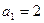 .
.故数列
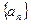 的通项公式为
的通项公式为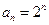
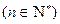 . ……………………………………….6分
. ……………………………………….6分(II)因
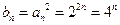 ,所以
,所以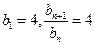
即数列
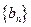 是首项为
是首项为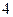 ,公比是
,公比是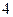 的等比数列.
的等比数列. 所以
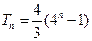 ,……………………………………….……………………………………7分
,……………………………………….……………………………………7分则
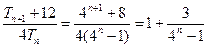
又
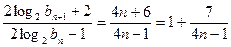 . ……………………………………8分
. ……………………………………8分
法一:数学归纳法
猜想
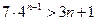
①当
 时,
时,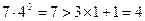 ,上面不等式显然成立;
,上面不等式显然成立;②假设当
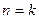 时,不等式
时,不等式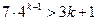 成立
成立当
 时,
时,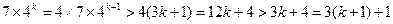 .
.综上①②对任意的
 均有
均有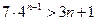 ……………………………………….10分
……………………………………….10分法二:二项式定理:因为
 ,
,所以
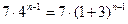
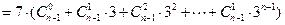
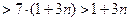 .
.即对任意的
 均有
均有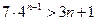 . ……………………………………..10分
. ……………………………………..10分又
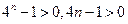 ,
, 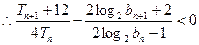
所以对任意的
 均有
均有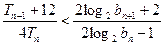 . …………………
. ………………… ……….12分
……….12分略

练习册系列答案
相关题目
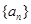 的前
的前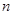 项和为
项和为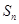 ,且
,且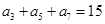 ,则
,则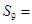 ( )
( )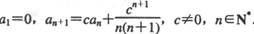 .
.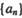 丨的通项:
丨的通项: ?
?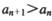 恒成立,求c的取值范围.
恒成立,求c的取值范围.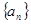 的通项公式为
的通项公式为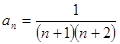 ,其前
,其前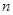 项和为
项和为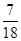 ,则
,则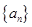 满足
满足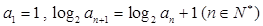 ,它的前
,它的前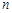 项和为
项和为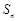 ,则
,则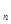 >1025
>1025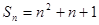 ,则
,则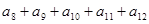 =___________.
=___________.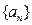 的通项公式是
的通项公式是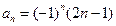 ,则它的前51项和是 ( )
,则它的前51项和是 ( )
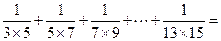
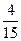
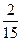
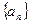 的通项公
的通项公 式
式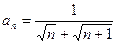 ,若其前
,若其前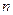 项和为10,则项数
项和为10,则项数