题目内容
(2013•湖南模拟)已知向量
=(sinx,2co
x),
=(2
cosx,-1),函数f(x)=
•
+1.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的
倍;再把所得到的图象向左平移
个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在区间[-
,
]上的值域.
| a |
| s | 2 |
| b |
| 3 |
| a |
| b |
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
分析:(1)利用数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式,进而即可得出周期及其单调区间;
(2)利用图象变换的法则即可得到y=g(x),再利用三角函数的单调性即可得出值域.
(2)利用图象变换的法则即可得到y=g(x),再利用三角函数的单调性即可得出值域.
解答:解:(1)f(x)=
•
+1=2
sinxcosx-2cos2x+1=
sin2x-cos2x=2sin(2x-
),
∴函数f(x)的最小正周期T=
=π,
由-
+2kπ≤2x-
≤2kπ+
,解得-
+kπ≤x≤kπ+
(k∈Z).
∴函数f(x)的单调递增区间为[-
+kπ,
+kπ](k∈Z);
(2)函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的
倍得到y=2sin(4x-
),
再把所得到的图象向左平移
个单位长度,得到函数y=g(x)=2sin[4(x+
)-
]=2cos4x,
当x∈[-
,
]时,4x∈[-
,
],
∴当x=0时,g(x)max=2;当x=-
时,g(x)min=2cos(-
)=-1.
∴函数y=g(x)在区间[-
,
]上的值域为[-1,2].
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
∴函数f(x)的最小正周期T=
| 2π |
| 2 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调递增区间为[-
| π |
| 6 |
| π |
| 3 |
(2)函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 6 |
再把所得到的图象向左平移
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
当x∈[-
| π |
| 6 |
| π |
| 12 |
| 2π |
| 3 |
| π |
| 3 |
∴当x=0时,g(x)max=2;当x=-
| π |
| 6 |
| 2π |
| 3 |
∴函数y=g(x)在区间[-
| π |
| 6 |
| π |
| 12 |
点评:熟练掌握数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式、三角函数周期及其单调性、图象变换的法则是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=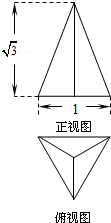 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )