题目内容
下列4个命题:
①命题“若am2<bm2(a,b,m∈R),则a<b”;
②“a≥
”是“对任意的正数x,2x+
≥1”的充要条件;
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x<0”;
④已知p,q为简单命题,则“p∧q为假命题”是“p∨q为假命题”的充分不必要条件.
其中正确命题的序号是
①命题“若am2<bm2(a,b,m∈R),则a<b”;
②“a≥
| 1 |
| 8 |
| a |
| x |
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x<0”;
④已知p,q为简单命题,则“p∧q为假命题”是“p∨q为假命题”的充分不必要条件.
其中正确命题的序号是
①②
①②
.分析:①由题意m2>0,根据不等式的性质可得结论;
②对任意的正数x,2x+
≥1成立,即a≥-2x2+x,又-2x2+x=-2(x-
)2+
≤
,故可得结论;
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0”;
④根据“p∧q为假命题”,一假即假,p∨q为假命题时,全假为假,即可得到结论.
②对任意的正数x,2x+
| a |
| x |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0”;
④根据“p∧q为假命题”,一假即假,p∨q为假命题时,全假为假,即可得到结论.
解答:解:①由题意m2>0,∴若am2<bm2(a,b,m∈R),根据不等式的性质可得a<b,故①正确;
②对任意的正数x,2x+
≥1成立,即a≥-2x2+x,又-2x2+x=-2(x-
)2+
≤
,∴a≥
,故②正确;
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0”,故③错误;
④已知p,q为简单命题,则“p∧q为假命题”时,p,q至少一个为假,所以p∨q为假命题或真命题,反之p∨q为假命题时,p,q均为假命题,故p∧q为假命题,所以“p∧q为假命题”是“p∨q为假命题”的必要不充分条件,故④错误.
综上知,正确的序号为①②
故答案为:①②
②对任意的正数x,2x+
| a |
| x |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
③命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0”,故③错误;
④已知p,q为简单命题,则“p∧q为假命题”时,p,q至少一个为假,所以p∨q为假命题或真命题,反之p∨q为假命题时,p,q均为假命题,故p∧q为假命题,所以“p∧q为假命题”是“p∨q为假命题”的必要不充分条件,故④错误.
综上知,正确的序号为①②
故答案为:①②
点评:本题考查命题真假判断,考查不等式的性质,含有量词的命题的否定,考查复合命题,解题时一一判断,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目

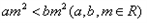 ,则a<b”;
,则a<b”;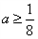 ”是“对任意的正数x ,
”是“对任意的正数x ,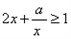 ”的充要条件;
”的充要条件;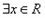 ,
, ”的否定是:“
”的否定是:“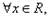
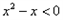 ”;
”;