题目内容
已知m∈R,直线l:mx-(m2+1)y=4m和圆C:x2+y2-8x+4y+16=0。
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为 的两段圆弧?请说明理由。
的两段圆弧?请说明理由。
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为
 的两段圆弧?请说明理由。
的两段圆弧?请说明理由。 解:(1)直线l的方程可化为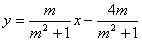 ,
,
于是直线l的斜率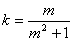 ,
,
因为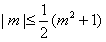 ,
,
所以,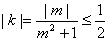 ,当且仅当|m|=1时等号成立。
,当且仅当|m|=1时等号成立。
所以,直线l的斜率k的取值范围是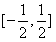 。
。
(2)不能,
由(1)知直线l的方程为:y=k(x-4),其中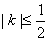 ,
,
圆C的方程可化为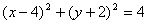 ,
,
所以,圆C的圆心为C(4,-2),半径r=2,
于是圆心C到直线l的距离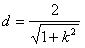 ,
,
由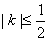 ,得
,得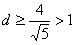 ,即
,即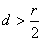 ,
,
所以,若直线l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于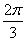 ,
,
故直线l不能将圆C分割成弧长的比值为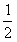 的两段弧。
的两段弧。
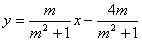 ,
, 于是直线l的斜率
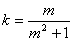 ,
,因为
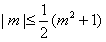 ,
,所以,
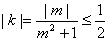 ,当且仅当|m|=1时等号成立。
,当且仅当|m|=1时等号成立。所以,直线l的斜率k的取值范围是
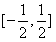 。
。(2)不能,
由(1)知直线l的方程为:y=k(x-4),其中
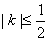 ,
, 圆C的方程可化为
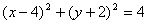 ,
,所以,圆C的圆心为C(4,-2),半径r=2,
于是圆心C到直线l的距离
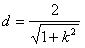 ,
,由
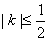 ,得
,得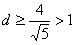 ,即
,即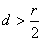 ,
,所以,若直线l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于
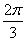 ,
,故直线l不能将圆C分割成弧长的比值为
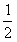 的两段弧。
的两段弧。
练习册系列答案
相关题目