题目内容
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(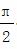 ,-2).
,-2).
(1)求φ的值;
(2)若f(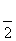 )=
)=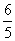 ,-
,-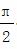 <α<0,求sin(2α-
<α<0,求sin(2α-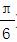 )的值.
)的值.
解:(1)因为函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点( ,-2),
,-2),
所以f( )=2sin(π+φ)=-2,
)=2sin(π+φ)=-2,
即sinφ=1.
因为0<φ<2π,所以φ= .
.
(2)由(1)得,f(x)=2cos2x.
因为f(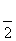 )=
)=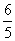 ,所以cosα=
,所以cosα= .
.
又因为 <α<0,所以sinα=-
<α<0,所以sinα=-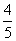 .
.
所以sin2α=2sinαcosα=- ,cos2α=2cos2α-1=-
,cos2α=2cos2α-1=- .…
.…
从而sin(2α- )=sin2αcos
)=sin2αcos -cos2αsin
-cos2αsin =
= . 分
. 分

练习册系列答案
相关题目
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
 上的奇函数
上的奇函数 ,满足
,满足 ,且在区间
,且在区间 上是增函数,若方程
上是增函数,若方程 ,在区间
,在区间 上有四个不同的根
上有四个不同的根 ,则
,则 =( )
=( ) ,第二年的增长率为
,第二年的增长率为 ,则该市这两年生产总值的年平均增长率为( )
,则该市这两年生产总值的年平均增长率为( ) B.
B.
 D.
D.
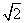 c=2b,sinB=
c=2b,sinB= R.
R. ,
, ,则集合
,则集合 等于
等于  B.
B. C.
C.  D.
D.
 的图象与直线
的图象与直线 及
及 轴所围成图形的面积称为函数
轴所围成图形的面积称为函数 在
在 上的面积,已知函数
上的面积,已知函数 在
在 上的面积为
上的面积为 ,则函数
,则函数 在
在 上的面积为_____________。
上的面积为_____________。