题目内容
已知数列{an}的首项为a1=3,通项an与前n项和sn之间满足2an=Sn•Sn-1(n≥2).
(1)求证:数列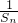 是等差数列;
是等差数列;
(2)求数列{an}的通项公式;
(3)求数列{an}中的最大项.
解(1)由2an=Sn•Sn-1(n≥2),得2(Sn-Sn-1)=Sn•Sn-1.
所以 (n≥2),
(n≥2),
所以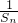 是等差数列;
是等差数列;
(2)由(1)知, ,
,
所以 ,
,
当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1= ,
,
∴ ;
;
(3)由a1,a2,a3及n≥3时an的单调性知: 是最大项;
是最大项;
分析:(1)把2an=Sn•Sn-1(n≥2)中的an化为Sn-Sn-1,然后两边同除以Sn•Sn-1.结合等差数列定义可证;
(2)由(1)可求得Sn,根据 即可求得{an}的通项公式;
即可求得{an}的通项公式;
(3)根据n≥3时an的单调性及前三项即可求得最大项;
点评:本题考查利用数列递推公式求数列通项、等差数列的定义及其判断等知识,属中档题.
所以
 (n≥2),
(n≥2),所以
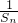 是等差数列;
是等差数列;(2)由(1)知,
 ,
,所以
 ,
,当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1=
 ,
,∴
 ;
;(3)由a1,a2,a3及n≥3时an的单调性知:
 是最大项;
是最大项;分析:(1)把2an=Sn•Sn-1(n≥2)中的an化为Sn-Sn-1,然后两边同除以Sn•Sn-1.结合等差数列定义可证;
(2)由(1)可求得Sn,根据
 即可求得{an}的通项公式;
即可求得{an}的通项公式;(3)根据n≥3时an的单调性及前三项即可求得最大项;
点评:本题考查利用数列递推公式求数列通项、等差数列的定义及其判断等知识,属中档题.

练习册系列答案
相关题目