题目内容
已知函数 有且仅有两个不同的零点
有且仅有两个不同的零点 ,
, ,则( )
,则( )
A.当 时, 时, , , |
B.当 时, 时, , , |
C.当 时, 时, , , |
D.当 时, 时, , , |
B
解析试题分析:函数求导,得: ,得两个极值点:
,得两个极值点:
因为函数f(x)过定点(0,-2),有且仅有两个不同的零点,所以,可画出函数图象如下图:
因此,可知, ,只有B符合.
,只有B符合. .
.
考点:导数的应用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知函数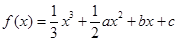 在
在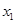 处取得极大值,在
处取得极大值,在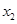 处取得最小值,满足
处取得最小值,满足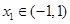 ,
,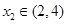 ,则
,则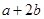 的取值范围是( )
的取值范围是( )
A.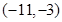 | B.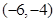 | C.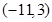 | D. |
已知定义在 上的函数
上的函数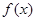 满足
满足 ,且
,且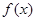 的导函数
的导函数 在
在 上恒有
上恒有 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D.  |
已知函数f(x)(x∈R)满足 >f(x),则 ( )
>f(x),则 ( )
A.f(2)< f(0) f(0) | B.f(2)≤ f(0) f(0) |
C.f(2)= f(0) f(0) | D.f(2)> f(0) f(0) |
已知函数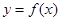 是定义在数集
是定义在数集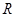 上的奇函数,且当
上的奇函数,且当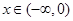 时,
时,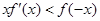 成立,若
成立,若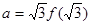 ,
,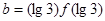 ,
,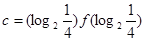 ,则
,则 的大小关系是( )
的大小关系是( )
A.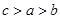 | B.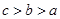 | C.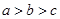 | D.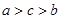 |
设 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )
| A.±1 | B.±2 | C.± | D.2 |
已知函数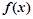 定义在R上的奇函数,当
定义在R上的奇函数,当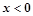 时,
时,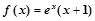 ,给出下列命题:
,给出下列命题:
①当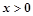 时,
时, ②函数
②函数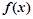 有2个零点
有2个零点
③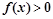 的解集为
的解集为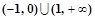 ④
④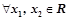 ,都有
,都有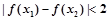
其中正确命题个数是( )
| A.1 | B.2 | C.3 | D.4 |
设直线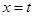 与函数
与函数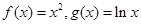 的图象分别交于点
的图象分别交于点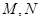 ,则当
,则当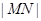 达到最小时
达到最小时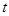 的值为( )
的值为( )
| A.1 | B.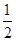 | C.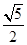 | D.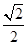 |
设曲线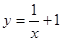 在点(1,2)处的切线与直线
在点(1,2)处的切线与直线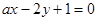 平行,则
平行,则 =( )
=( )
| A.-1 | B.0 | C.-2 | D.2 |