题目内容
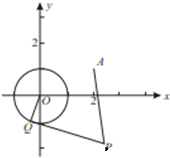 已知点E(-2,0),F(2,0),曲线C上的动点M满足
已知点E(-2,0),F(2,0),曲线C上的动点M满足| ME |
| MF |
(Ⅰ)求线段PA的最小值;
(Ⅱ)若以P为圆心所作的⊙P与曲线C有公共点,试求半径取最小值时⊙P的标准方程.
分析:(Ⅰ)设出M的坐标,利用向量的数量积公式化简,可得曲线C的方程;求出P的坐标之间的关系,表示出线段PQ长,利用配方法可求PQ的最小值;
(Ⅱ)根据P为圆心所作的圆P与曲线C有公共点,确定半径的范围,利用配方法,即可求半径取最小值时圆P的标准方程.
(Ⅱ)根据P为圆心所作的圆P与曲线C有公共点,确定半径的范围,利用配方法,即可求半径取最小值时圆P的标准方程.
解答: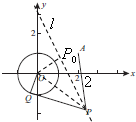 解:(Ⅰ)设M(x,y),则
解:(Ⅰ)设M(x,y),则
=(x+2,y),
=(x-2,y),
∴
•
=(x+2,y)•(x-2,y)=x2-4+y2=-3,
即M点轨迹(曲线C)方程为 x2+y2=1,
即曲线C是以原点为圆心的单位圆.
连OP,∵Q为切点,PQ⊥OQ,由勾股定理有:PQ2=OP2-OQ2.
又由已知PQ=PA,
故PQ2=PA2.
即:a2+b2-1=(a-2)2+(b-1)2,
化简得实数a、b间满足的等量关系为:2a+b-3=0,即b=-2a+3.
∴PQ=
=
=
=
,
故当a=
时,PQ取得最小值为
即线段PQ长的最小值为
.
(Ⅱ)设圆P的半径为R,则
∵圆P与圆O有公共点,圆O的半径为1,
∴|R-1|≤|OP|≤R+1,
即R≥|OP|-1且R≤|OP|+1.
而|OP|=
=
=
,
故当a=
时,|OP|min=
.
此时b=-2a+3=
,Rmin=
-1.
∴半径取最小值时圆P的标准方程为(x-
)2+(y-
)2=(
-1)2.
 解:(Ⅰ)设M(x,y),则
解:(Ⅰ)设M(x,y),则| EM |
| FM |
∴
| EM |
| FM |
即M点轨迹(曲线C)方程为 x2+y2=1,
即曲线C是以原点为圆心的单位圆.
连OP,∵Q为切点,PQ⊥OQ,由勾股定理有:PQ2=OP2-OQ2.
又由已知PQ=PA,
故PQ2=PA2.
即:a2+b2-1=(a-2)2+(b-1)2,
化简得实数a、b间满足的等量关系为:2a+b-3=0,即b=-2a+3.
∴PQ=
| a2+b2-1 |
| a2+(-2a+3)2-1 |
| 5a2-12a+8 |
5(a-
|
故当a=
| 6 |
| 5 |
2
| ||
| 5 |
2
| ||
| 5 |
(Ⅱ)设圆P的半径为R,则
∵圆P与圆O有公共点,圆O的半径为1,
∴|R-1|≤|OP|≤R+1,
即R≥|OP|-1且R≤|OP|+1.
而|OP|=
| a2+b2 |
| a2+(-2a+3)2 |
5(a-
|
故当a=
| 6 |
| 5 |
3
| ||
| 5 |
此时b=-2a+3=
| 3 |
| 5 |
3
| ||
| 5 |
∴半径取最小值时圆P的标准方程为(x-
| 6 |
| 5 |
| 3 |
| 5 |
3
| ||
| 5 |
点评:本题考查圆的方程,考查轨迹方程,考查向量知识的运用,考查圆与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
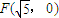 的双曲线的右支,已知它的一条渐近线方程是
的双曲线的右支,已知它的一条渐近线方程是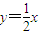 .
.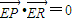 ,求证:直线l过一个定点,并求出定点的坐标.
,求证:直线l过一个定点,并求出定点的坐标.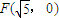 的双曲线的右支,已知它的一条渐近线方程是
的双曲线的右支,已知它的一条渐近线方程是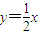 .
.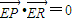 ,求证:直线l过一个定点,并求出定点的坐标.
,求证:直线l过一个定点,并求出定点的坐标.