题目内容
曲线C是中心在原点,焦点为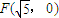 的双曲线的右支,已知它的一条渐近线方程是
的双曲线的右支,已知它的一条渐近线方程是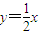 .
.(1)求曲线C的方程;
(2)已知点E(2,0),若直线l与曲线C交于不同于点E的P,R两点,且
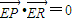 ,求证:直线l过一个定点,并求出定点的坐标.
,求证:直线l过一个定点,并求出定点的坐标.
【答案】分析:(1)可设曲线C的方程为 ,由题意可得,a=2b,a2+b2=5,从而可求a,b,进而可求曲线C的方程
,由题意可得,a=2b,a2+b2=5,从而可求a,b,进而可求曲线C的方程
(2)设P(x1,y1),R(x2,y2),当直线l的斜率存在时,设直线l的方程为y=kx+m,由 ,,由方程的根与系数关系及
,,由方程的根与系数关系及 =(x1-2)(x2-2)+(kx1+m)(kx2+m)=0,代入可求得k,m之间的关系则直线l由直线方程的点斜式可求直线所过的定点;当直线l的斜率不存在时,x1=x2,y1=-y2,,由
=(x1-2)(x2-2)+(kx1+m)(kx2+m)=0,代入可求得k,m之间的关系则直线l由直线方程的点斜式可求直线所过的定点;当直线l的斜率不存在时,x1=x2,y1=-y2,,由 ,代入可求
,代入可求
解答:解:(1)设曲线C的方程为
∵一条渐近线方程是 ,c=
,c=
∴a=2b,a2+b2=c2=5
∴a=2,b=1
故所求曲线C的方程是 …(5分)
…(5分)
(2)设P(x1,y1),R(x2,y2),
①当直线l的斜率存在时,设直线l的方程为y=kx+m
由 ,
,
此时1-4k2≠0
∴ …(7分)
…(7分)
由
=(x1-2)(x2-2)+(kx1+m)(kx2+m)=0
∴(1+k2)x1x2+(km-2)(x1+x2)+m2+4=0
(1+k2)• +(km-2)•
+(km-2)• +m2+4=0
+m2+4=0
整理有 …(10分)
…(10分)
当m=-2k时,直线L过点E,不合题意
当m=- ,则直线l的方程为
,则直线l的方程为
则直线l过定点( )…(12分)
)…(12分)
②当直线l的斜率不存在时,x1=x2,y1=-y2,
由 ,
,
有
从而有 .此时直线L过点
.此时直线L过点
故直线l过定点 …(15分)
…(15分)
点评:本题主要考查了由双曲线的性质求解双曲线的方程,直线与双曲线的相交关系的应用,方程的根与系数关系的应用,向量的坐标表示的应用,属于直线与曲线位置关系的综合应用,属于综合性试题.
 ,由题意可得,a=2b,a2+b2=5,从而可求a,b,进而可求曲线C的方程
,由题意可得,a=2b,a2+b2=5,从而可求a,b,进而可求曲线C的方程(2)设P(x1,y1),R(x2,y2),当直线l的斜率存在时,设直线l的方程为y=kx+m,由
 ,,由方程的根与系数关系及
,,由方程的根与系数关系及 =(x1-2)(x2-2)+(kx1+m)(kx2+m)=0,代入可求得k,m之间的关系则直线l由直线方程的点斜式可求直线所过的定点;当直线l的斜率不存在时,x1=x2,y1=-y2,,由
=(x1-2)(x2-2)+(kx1+m)(kx2+m)=0,代入可求得k,m之间的关系则直线l由直线方程的点斜式可求直线所过的定点;当直线l的斜率不存在时,x1=x2,y1=-y2,,由 ,代入可求
,代入可求解答:解:(1)设曲线C的方程为

∵一条渐近线方程是
 ,c=
,c=
∴a=2b,a2+b2=c2=5
∴a=2,b=1
故所求曲线C的方程是
 …(5分)
…(5分)(2)设P(x1,y1),R(x2,y2),
①当直线l的斜率存在时,设直线l的方程为y=kx+m
由
 ,
,此时1-4k2≠0
∴
 …(7分)
…(7分)由

=(x1-2)(x2-2)+(kx1+m)(kx2+m)=0
∴(1+k2)x1x2+(km-2)(x1+x2)+m2+4=0
(1+k2)•
 +(km-2)•
+(km-2)• +m2+4=0
+m2+4=0整理有
 …(10分)
…(10分)当m=-2k时,直线L过点E,不合题意
当m=-
 ,则直线l的方程为
,则直线l的方程为
则直线l过定点(
 )…(12分)
)…(12分)②当直线l的斜率不存在时,x1=x2,y1=-y2,
由
 ,
,有

从而有
 .此时直线L过点
.此时直线L过点
故直线l过定点
 …(15分)
…(15分)点评:本题主要考查了由双曲线的性质求解双曲线的方程,直线与双曲线的相交关系的应用,方程的根与系数关系的应用,向量的坐标表示的应用,属于直线与曲线位置关系的综合应用,属于综合性试题.

练习册系列答案
相关题目