题目内容
已知△ABC在第一象限,A(1,1),B(5,1),∠A=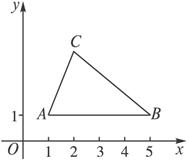
(1)AB所在直线的方程;
(2)AC和BC所在直线的方程;
(3)AC、BC所在直线与y轴交点间的距离.
思路分析:求AB的方程时,先观察两点坐标易得AC、BC,通过画图易求其斜率,然后由点斜式写出即可.
解:(1)∵kAB=![]() =0,
=0,
∴AB所在直线方程为y=1.
(2)∵kAC=tan![]() =
=![]() ,
,
∴AC所在直线方程为y-1=![]() (x-1),
(x-1),
即![]() x-y+1-
x-y+1-![]() =0.
=0.
又kBC=tan(π-![]() )=-1,
)=-1,
∴BC所在直线方程为y-1=-(x-5),
即x+y-6=0.
(3)由直线AC的方程为![]() x-y+1-
x-y+1-![]() =0,
=0,
令x=0,则y=1-![]() .
.
由直线BC的方程x+y-6=0,
令x=0,则y=6.
∴两交点间的距离为|6-1+![]() |=5+
|=5+![]() .
.

练习册系列答案
相关题目
 ,2) (B)(0,2)
(C)(
,2) (B)(0,2)
(C)( ,由图象可知当直线
,由图象可知当直线 经过点B时,截距最大,此时
经过点B时,截距最大,此时 ,当直线经过点C时,直线截距最小.因为
,当直线经过点C时,直线截距最小.因为 轴,所以
轴,所以 ,三角形的边长为2,设
,三角形的边长为2,设 ,则
,则 ,解得
,解得 ,
, ,因为顶点C在第一象限,所以
,因为顶点C在第一象限,所以 ,即
,即 代入直线
代入直线 得
得 ,所以
,所以 的取值范围是
的取值范围是 ,选A.
,选A. =(
=( ),
), =(
=(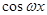 ,
,
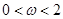 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
. 的表达式及单调递增区间;
的表达式及单调递增区间; =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
 ,……11分故
,……11分故