Question

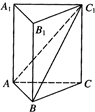如图，在正三棱柱ABC-A₁B₁C₁中，AB=2，若二面角C-AB-C₁的大小为60°，则异面直线A₁B₁和BC₁所成角的余弦值为（　　）

• A、

  1

  2

• B、

  3

  2

• C、

  7

  7

• D、

  13

  13

Answer 1

分析：取AB的中点D，连接CD，C₁D，利用AB∥A₁B₁，将异面直线A₁B₁和BC₁所成角转化为异面直线AB和BC₁所成角，在△ABC₁中解决．

解答：解：如图取AB的中点D，连接CD，C₁D，则有CD⊥AB，C₁D⊥AB，∴∠C₁DC=60°，CD=

3

，CC1=CDtan60°=3，AC1=BC1=

32+22

=

13

．在△ABC₁中，cos∠ABC₁=

AB2+B C 2 1 -A C 2 1

2AB•BC1

=

13

13

，∵AB∥A₁B₁，因此∠ABC₁是直线A₁B₁与BC₁所成的角或补角，
因此直线A₁B₁与BC₁所成的角的余弦值是

13

13

故选D．

点评：本题考查正三棱柱的性质、二面角的意义及异面直线所成的角．解决的关键是将空间角化为平面角，在三角形当中去解决．