题目内容
若a>0,b>0,且函数f(x)=4x3-ax2-bx-2在x=1处有极值,则ab的最大值 .
【答案】分析:根据函数f(x)在x=1处取得极值,得到关于a,b的等量关系,再用基本不等式即可求出最值.
解答:解:f′(x)=12x2-2ax-b,
因为f(x)在x=1处有极值,
所以f′(1)=0,即12-2a-b=0,也即2a+b=12.
又a>0,b>0,
所以2a•b≤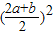 =
=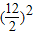 =36,当且仅当2a=b=6,即a=3,b=6时取等号.
=36,当且仅当2a=b=6,即a=3,b=6时取等号.
所以ab≤18,即ab的最大值为18.
故答案为:18.
点评:本题考查函数在某点取得极值的条件及应用基本不等式求最值问题,运用基本不等式求最值要注意使用条件:一正、二定、三相等.
解答:解:f′(x)=12x2-2ax-b,
因为f(x)在x=1处有极值,
所以f′(1)=0,即12-2a-b=0,也即2a+b=12.
又a>0,b>0,
所以2a•b≤
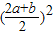 =
=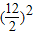 =36,当且仅当2a=b=6,即a=3,b=6时取等号.
=36,当且仅当2a=b=6,即a=3,b=6时取等号.所以ab≤18,即ab的最大值为18.
故答案为:18.
点评:本题考查函数在某点取得极值的条件及应用基本不等式求最值问题,运用基本不等式求最值要注意使用条件:一正、二定、三相等.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A、2 | B、3 | C、6 | D、9 |