题目内容
(本题10分)在直角坐标系xOy中,曲线C1的参数方程为 (α为参数)M是C1上的动点,P点满足
(α为参数)M是C1上的动点,P点满足 =2
=2 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的参数方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
【答案】
(1) ;(2)
;(2) .
.
【解析】第一问中设P(x,y),则由条件知M ,由于M点在C1上,所以
,由于M点在C1上,所以

第二问曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ= 与C1的交点A的极径为ρ1=4sin
与C1的交点A的极径为ρ1=4sin ,
,
射线θ= 与C2的交点B的极径为ρ2=8sin
与C2的交点B的极径为ρ2=8sin .
.
所以|AB|=|ρ1-ρ2|= .
.
解: (1)设P(x,y),则由条件知M ,由于M点在C1上,所以
,由于M点在C1上,所以

从而C2的参数方程为
 (α为参数)
(α为参数)
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ= 与C1的交点A的极径为ρ1=4sin
与C1的交点A的极径为ρ1=4sin ,
,
射线θ= 与C2的交点B的极径为ρ2=8sin
与C2的交点B的极径为ρ2=8sin .
.
所以|AB|=|ρ1-ρ2|= .
.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 中,角
中,角 的顶点为坐标原点,始边在
的顶点为坐标原点,始边在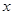 轴的正半轴上,当角
轴的正半轴上,当角 :
: =3
=3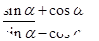 的值; (2)
的值; (2) 的值.
的值. 的参数方程为
的参数方程为 .以坐标原点为极点,
.以坐标原点为极点, 轴的正半轴为极轴的极坐标系中.曲线
轴的正半轴为极轴的极坐标系中.曲线 的极坐标方程为
的极坐标方程为 .
. 化成普通方程和直角坐标方程;并说明它们分别表示什么曲线.
化成普通方程和直角坐标方程;并说明它们分别表示什么曲线. ,使点
,使点 中,直线
中,直线 的参数方程为
的参数方程为 为参数),若以O为极点,
为参数),若以O为极点, 轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 ,求直线
,求直线 中,直线
中,直线 的参数方程为
的参数方程为 为参数),若以O为极点,
为参数),若以O为极点,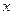 轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 ,求直线
,求直线